定義
在數論,狄利克雷定理說明對於任意互質的正整數a,d,有無限多個質數的形式如a + nd,其中n為正整數,即在算術級數a + d,a + 2d,a + 3d,...中有無限多個質數——有無限個質數模d同餘a。相關定理
歐幾里得證明了有無限個質數,即有無限多個質數的形式如2n + 1。算術級數的質數定理:若a,d互質,則有
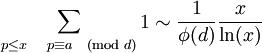 相關
相關。
其中φ是歐拉φ函式。取d = 2,可得一般的質數定理。
Linnik定理說明了級數中最小的質數的範圍:算術級數a + nd中最小的質數少於cd^L,其中L和c均為常數,但這兩個常數的最小值尚未找到。
Chebotarev密度定理是在狄利克雷定理在伽羅瓦擴張的推廣。
歷史
歐拉曾以(見左圖),來證明質數有無限個。約翰·彼得·狄利克雷得以靈感,藉助證明來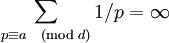 歷史
歷史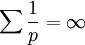 歷史
歷史