定義
質數又稱素數。一個大於1的自然數,除了1和它自身外,不能整除其他自然數的數叫做質數;否則稱為合數。
性質
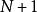 質數
質數質數的個數是無窮的。歐幾里得的《幾何原本》中有一個經典的證明。它使用了證明常用的方法:反證法。具體證明如下:假設質數只有有限的n個,從小到大依次排列為p,p,……,p,設N=p×p×……×p,那么, 是素數或者不是素數。
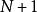 質數
質數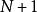 質數
質數如果 為素數,則 要大於p,p,……,p,所以它不在那些假設的素數集合中。
1、如果 為合數,因為任何一個合數都可以分解為幾個素數的積;而N和N+1的最大公約數是1,所以不可能被p,p,……,p整除,所以該合數分解得到的素因數肯定不在假設的素數集合中。因此無論該數是素數還是合數,都意味著在假設的有限個素數之外還存在著其他素數。所以原先的假設不成立。也就是說,素數有無窮多個。
2、其他數學家給出了一些不同的證明。歐拉利用黎曼函式證明了全部素數的倒數之和是發散的,恩斯特·庫默的證明更為簡潔,哈里·弗斯滕伯格則用拓撲學加以證明。
分布規律
以36N(N+1)為單位,隨著N的增大,素數的個數以波浪形式漸漸增多。
孿生質數也有相同的分布規律。
以下15個區間內質數和孿生質數的統計數。
S1區間1——72,有素數18個,孿生素數7對。(2和3不計算在內,最後的數是孿中的也算在前面區間。)
S2區間73——216,有素數27個,孿生素數7對。
S3區間217——432,有素數36個,孿生素數8對。
S4區間433——720,有素數45個,孿生素數7對。
S5區間721——1080,有素數52個,孿生素數8對。
S6區間1081——1512,素數60個,孿生素數9對。
S7區間1513——2016,素數65個,孿生素數11對。
S8區間2017——2592,素數72個,孿生素數12對。
S9區間2593——3240,素數80個,孿生素數10對。
S10區間3241——3960,素數91個,孿生素數19對。
S11區間3961——4752素數92個,孿生素數17對。
S12區間4752——5616素數98個,孿生素數13對。
S13區間5617——6552素數108個,孿生素數14對。
S14區間6553——7560素數113個,孿生素數19對。
S15區間7561——8640素數116個,孿生素數14對。
素數分布規律的發現,許多素數問題可以解決。
數目計算
儘管整個素數是無窮的,仍然有人會問“100,000以下有多少個素數?”,“一個隨機的100位數多大可能是素數?”。素數定理可以回答此問題。
1、在一個大於1的數 a和它的2倍之間(即區間(a, 2a]中)必存在至少一個素數。
2、存在任意長度的素數等差數列。
3、一個偶數可以寫成兩個合數之和,其中每一個合數都最多只有9個質因數。(挪威數學家布朗,1920年)
4、一個偶數必定可以寫成一個質數加上一個合成數,其中合數的因子個數有上界。(瑞尼,1948年)
5、一個偶數必定可以寫成一個質數加上一個最多由5個因子所組成的合成數。後來,有人簡稱這結果為 (1 + 5)(中國潘承洞,1968年)
6、一個充分大偶數必定可以寫成一個素數加上一個最多由2個質因子所組成的合成數。簡稱為 (1 + 2)
性質
質數具有許多獨特的性質:
(1)質數p的約數只有兩個:1和p。
(2)初等數學基本定理:任一大於1的自然數,要么本身是質數,要么可以分解為幾個質數之積,且這種分解是唯一的。
(3)質數的個數是無限的。
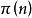 質數
質數(4)質數的個數公式 是不減函式。
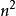 質數
質數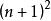 質數
質數(5)若n為正整數,在 到 之間至少有一個質數。
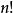 質數
質數(6)若n為大於或等於2的正整數,在n到 之間至少有一個質數。
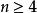 質數
質數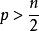 質數
質數(7)若質數p為不超過n( )的最大質數,則 。
(8)所有大於10的質數中,個位數只有1,3,7,9。
公式
素數密度公式
 100以內的素數
100以內的素數根據
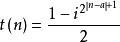 質數
質數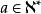 質數
質數構造函式 a為常數 且 1-1
根據1-1 性質 以多項式
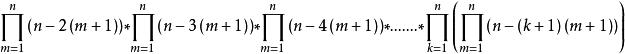 質數
質數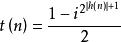 質數
質數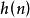 質數
質數為函式 中的指數
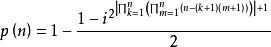 質數
質數得: 1-2
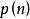 質數
質數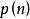 質數
質數當 n 為素數或 1 時, 等於 1,當 n 為合數時, 等於 0
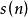 質數
質數得素數密度公式
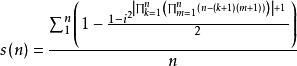 質數
質數式中 1 定義為素數。
通項公式
素數及偽素數通項公式
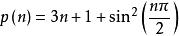 質數
質數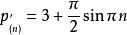 質數
質數把它拓展到實數那么它的切線為:
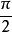 質數
質數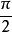 質數
質數由切線方程知,素數永遠在斜率3的折線上擺動,最大斜率3+ ,最小斜率3- 。
素數的變數n的通項公式
有以上公式能夠確定偽素數及素數,那么通過對其變數n的識別,我們可以寫出任意素數或偽素數
先確定偽素數的變數n,用n(x,y)來表示它,變數是個三維變數,公式如下:
n為偶數時:x,y 均自然數
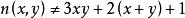 質數
質數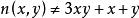 質數
質數n為奇數時:
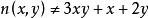 質數
質數滿足以上條件時是P(n)為素數。
套用
質數被利用在密碼學上,所謂的公鑰就是將想要傳遞的信息在編碼時加入質數,編碼之後傳送給收信人,任何人收到此信息後,若沒有此收信人所擁有的密鑰,則解密的過程中(實為尋找素數的過程),將會因為找質數的過程(分解質因數)過久,使即使取得信息也會無意義。
在汽車變速箱齒輪的設計上,相鄰的兩個大小齒輪齒數設計成質數,以增加兩齒輪內兩個相同的齒相遇嚙合次數的最低公倍數,可增強耐用度減少故障。
在害蟲的生物生長周期與殺蟲劑使用之間的關係上,殺蟲劑的質數次數的使用也得到了證明。實驗表明,質數次數地使用殺蟲劑是最合理的:都是使用在害蟲繁殖的高潮期,而且害蟲很難產生抗藥性。
以質數形式無規律變化的飛彈和魚雷可以使敵人不易攔截。
多數生物的生命周期也是質數(單位為年),這樣可以最大程度地減少碰見天敵的機會。
編程
基本判斷思路
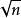 質數
質數在一般領域,對正整數n,如果用2到 之間的所有整數去除,均無法整除,則n為質數。
質數大於等於2 不能被它本身和1以外的數整除
代碼
Python 代碼:
Java代碼:
Php代碼:
C#代碼:
C代碼:
C/C++代碼:
Pascal代碼:
Javascript代碼:
Go代碼:
Basic 代碼
ALGOL代碼
素性檢測
上下素性判決定法:
首先,本文英文字母都表示整數,上半部B 》3N 》W,下半部B 》W 》3N。大於3的素數只有6N-1和6N+1兩種形式,我們只需判定這兩種數是素數還是合數即可。
命題 1 對於B=36N+1 型數而言。
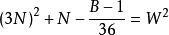 質數
質數若不定方程 有整數解,
則 6(3N-W)+1 是小因子數;6(3N+W)+1 是大因子數。
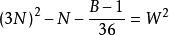 質數
質數若不定方程 有整數解,
則 6(3N-W)-1 是小因子數;6(3N+W)-1 是大因子數。
兩式都無解,是素數。
命題 2對於B=36N+7 形數而言。
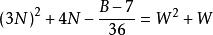 質數
質數若不定方程 有整數解,
則 6(3N-W)+1 是小因子數,6(3N+W+1)+1 是大因子數。
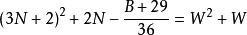 質數
質數若不定方程 有整數解,
則 6(3N+2-W)-1 是小因子數,6(3N+W+3)-1 是大因子數。
兩式都無解,是素數。
命題 3對於B=36N+13 形數而言。
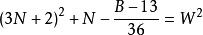 質數
質數若不定方程 有整數解,
則 6(3N+1-W)+1 是小因子數,6(3N+1+W)+1是大因子數。
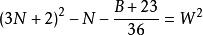 質數
質數若不定方程 有整數解,
則 6(3N+2-W)-1 是小因子數,6(3N+2+W)-1是大因子數。
兩式都無解,是素數。
命題 4 對於B=36N+19 形數而言。
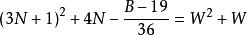 質數
質數若不定方程 有整數解,
則 6(3N+1-W)+1 是小因子數;6(3N+2+W)+1 是大因子數。
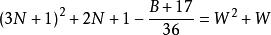 質數
質數若不定方程 有整數解,
則 6(3N+1-W)-1 是小因子數;6(3N+2+W)-1 是大因子數。
兩式都無解,是素數。
命題 5 對於B=36N+25 形數而言。
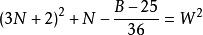 質數
質數若不定方程 有整數解,
則 6(3N+2-W)+1 是小因子數,6(3N+2+W)+1 是大因子數。
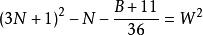 質數
質數若不定方程 有整數解,
則 6(3N+1-W)-1 是小因子數,6(3N+1+W)-1 是大因子數。
兩式都無解,是素數。
命題 6 對於B=36N+31 形數而言。
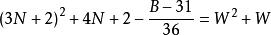 質數
質數若不定方程 有整數解,
則 6(3N+2-W)+1 是小因子數,6(3N+3+W)+1是大因子數。
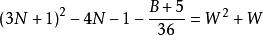 質數
質數若不定方程 有整數解,
則 6(3N-W)-1 是小因子數,6(3N+1+W)-1是大因子數。
兩式都無解,是素數。
命題 7對於B=36N-1 形數而言。
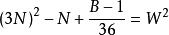 質數
質數若不定方程 有整數解,應該是(B+1)
則 6(3N-W)+1 是小因子數;6(3N+W)-1 是大因子數。
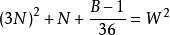 質數
質數若不定方程 有整數解,應該是(B+1)
則 6(W-3N)-1 是小因子數;6(W+3N)+1 是大因子數。
兩式都無解,是素數。
命題 8對於B=36N+5 形數而言。
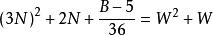 質數
質數若不定方程 有整數解,
則 6(W-3N)+1 是小因子數,6(W+3N+1)-1 是大因子數。
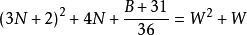 質數
質數若不定方程 有整數解,
則 6(W-3N-2)-1 是小因子數,6(W+3N+3)+1 是大因子數。
兩式都無解,是素數。
命題 9對於B=36N+11 形數而言。
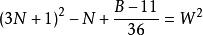 質數
質數若不定方程 有整數解,
則 6(W-3N-1)+1 是小因子數,6(W+3N+1)-1是大因子數。
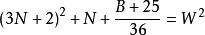 質數
質數若不定方程 有整數解,
則 6(W-3N-2)-1 是小因子數,6(W+3N+2)+1是大因子數。
兩式都無解,是素數。
命題 10 對於B=36N+17 形數而言。
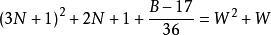 質數
質數若不定方程 有整數解,
則 6(W-3N-1)+1 是小因子數;6(W+3N+2)-1 是大因子數。
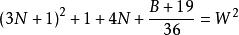 質數
質數若不定方程 有整數解,
則 6(W-3N-1)-1 是小因子數;6(W+3N+2)+1 是大因子數。
兩式都無解,是素數。
命題 11 對於B=36N+23 形數而言。
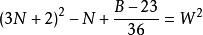 質數
質數若不定方程 有整數解,
則 6(W-3N-2)+1 是小因子數,6(W+3N+2)+1 是大因子數。
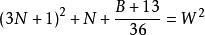 質數
質數若不定方程 有整數解,
則 6(W-3N-1)-1 是小因子數,6(W+3N+1)+1 是大因子數。
兩式都無解,是素數。
命題 12 對於B=36N+29 形數而言。
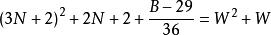 質數
質數若不定方程 有整數解,
則 6(W-3N-2)+1 是小因子數,6(W+3N+3)-1是大因子數。
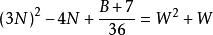 質數
質數若不定方程 有整數解,
則 6(W-3N)-1 是小因子數,6(W+3N+1)+1是大因子數。
兩式都無解,是素數。
素性檢測一般用於數學或者加密學領域。用一定的算法來確定輸入數是否是素數。不同於整數分解,素性測試一般不能得到輸入數的素數因子,只說明輸入數是否是素數。大整數的分解是一個計算難題,而素性測試是相對更為容易(其運行時間是輸入數字大小的多項式關係)。有的素性測試證明輸入數字是素數,而其他測試,比如米勒 - 拉賓(Miller–Rabin )則是證明一個數字是合數。因此,後者可以稱為合性測試。
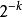 質數
質數素性測試通常是機率測試(不能給出100%正確結果)。這些測試使用除輸入數之外,從一些樣本空間隨機出去的數;通常,隨機素性測試絕不會把素數誤判為合數,但它有可能為把一個合數誤判為素數。誤差的機率可通過多次重複試驗幾個獨立值a而減小;對於兩種常用的測試中,對任何合數n,至少一半的a檢測n的合性,所以k的重複可以減小誤差機率最多到 ,可以通過增加k來使得誤差儘量小。
隨機素性測試的基本結構:
1、隨機選取一個數字a。
2、檢測某個包含a和輸入n的等式(與所使用的測試方法有關)。如果等式不成立,則n是合數,a作為n是合數的證據,測試完成。
3、從1步驟重複整個過程直到達到所設定的精確程度。
在幾次或多次測試之後,如果n沒有被判斷為合數,那么我們可以說n可能是素數。
常見的檢測算法:費馬素性檢驗(Fermat primality test),米勒拉賓測試(Miller–Rabin primality test) ,Solovay–Strassen測試,盧卡斯-萊默檢驗法(Lucas–Lehmer primality test)。
篩素數法
篩素數法可以比枚舉法節約極大量的時間(定n為所求最大值,m為≤n的質數個數,那么枚舉需要O(n^2)的時間複雜度,而篩素數法為O(m*n),顯然m<<n,所以時間效率有很大提升。)。如1000000的數據範圍,用篩素數法可在2s內解決。
思路:建立一個bool型數組M,若已知一個數M[k]是質數,那么其i(i為正整數)倍M[k*i]必然為合數,可將其去除。
篩選法的Java實現,如下:
採用簡單的埃氏篩選法和簡單的開方判斷素數法計算1000000以內素數的個數的效率比較:
StopWatch '計算1000000以內素數的個數': running time (millis) = 268
-----------------------------------------
ms % Task name
-----------------------------------------
00024 009% 簡單的埃氏篩選法;
00244 091% 簡單的開方判斷素數法。
猜想
哥德巴赫猜想:是否每個大於2的偶數都可寫成兩個素數之和?
孿生素數猜想:孿生素數就是差為2的素數對,例如11和13。是否存在無窮多的孿生素數?
斐波那契數列內是否存在無窮多的素數?
是否有無窮多個的梅森素數?
在n 與(n+1) 之間是否每隔n就有一個素數?
是否存在無窮個形式如X +1素數?
黎曼猜想
孿生素數無限多的證明
陰性合數定理和陰性素數定理
大於3的素數隻分布在6n-1和6n+1兩數列中。(n非0自然數,下同)
6n-1數列中的合數叫陰性合數,其中的素數叫陰性素數(q)。
6[6NM+(M-N)]-1=(6N+1)(6M-1)(N M兩個非0自然數,N=〈 M,下同)
6乘以陰性上等數減去1等於陰性上合數。
6[6NM-(M-N)]-1=(6N-1)(6M+1)
6乘以陰性下等數減去1等於陰性下合數。
在6n-1數列中只有這兩種合數,餘下就是陰性素數了,所以就有陰性素數定理
x=/=6NM+-(M-N)
陰性不等數不等於陰性上下兩式。
6x-1=q
6乘以陰性不等數減去1等於陰性素數。
陽性合數定理和陽性素數定理
6n+1數列中的合數叫陽性合數,其中的素數叫陽性素數(P)。
6[6NM+(N+M)]+1=(6N+1)(6M+1)
6乘以陽性上等數加上1等於陽性上合數。
6[6NM-(N+M)]+1=(6N-1)(6M-1)
6乘以陽性下等數加上1等於陽性下合數。
在6n+1數列中只有這兩種合數,餘下就是陽性素數了,所以就有陽性素數定理
X=/=6NM+-(N+M)
陽性不等數不等於陽性上下兩式。
6X+1=P
6乘以陽性不等數加上1等於陽性素數。
與孿生素數相對應的完全不等數
(X)=/=6NM+-(M+-N)
完全不等數,它既不等於陰性上下兩式;也不等於陽性上下兩式。
6(X)+1=P
6乘以完全不等數加上1等於陽性素數;
6(X)-1=q
6乘以完全不等數減去1等於陰性素數。
一個完全不等數所產生的陰性素數q和陽性素數P就是一對孿生素數.
並且完全不等數與孿生素數是一一對應的.
四。陰陽四種等數在自然數列中的分布概況
6NM+(M-N)=陰性上等數 6NM-(M-N)=陰性下等數
6NM+(N+M)=陽性上等數 6NM-(N+M)=陽性下等數
為了搞清它們在自然數中分布情況,把四式中的N叫級別因子數,M叫無限因子數。
四種等數的每一個級別的最小等數都在6NN+-(N+N)範圍。
每一級別的上等數相鄰兩等數距離是6n+1,在自然數列中比例是1/(6n+1),陰陽兩種上等數每個級別的比例合計是2/(6n+1),(但實際是略少於這個比例,因每一級別的底部都沒有這個級別的等數。)
每一級別的下等數相鄰等數的距離是6n-1,在自然數列中的比例是1/(6n-1),陰陽兩種下等數的每個級別的合計比例是2/(6n-1),(但實際是略少於這個比例,因每一級別的底部都沒有這個級別的等數。)
在相對應的級別標準單位的連續自然數篩掉一個級別的四種等數後,剩下非該級別的自然數的比例是[(6N-1)(6N-3)]/[(6N+1)(6N-1)].並且是精準的。
四種等數大小數列的互相滲透
自然數列中在陰性方面有陰性上等數數列和陰性的下等數數列;自然數數列在陽性方面陽性上等數數列和陽性下等數數列。它們的級別有無限多,每一個級別的數列的等數也是無限多的。同一種等數級別不同的數列都是互相滲透而產生重疊,並以兩級別的等數距離的乘積而嚴格地重疊的。篩掉N及以下級別的等數用連乘式正好可以表示它們的滲透重疊關係。
四種等數數列之間都有互相滲透而重疊,只有同一級別陰陽上上數列.下下數列沒有滲透。
如第一級別的陽性下等數,從4開始每隔5個自然數就是一個第一級別的陽性下等數,它的比例是1/5,只要大於3的任何連續5個自然數,第一級別陽性下等數的比例是1/5,並且永遠不變。第一級別的陰性下等數從6開始每隔5個個自然數就是一個陰性下等數,它的比例是1/5,只要大於5的連續5個自然數,第一級別陰性下等數的1/5的比例也是永恆的。這樣第一級別的陰陽兩種下等數的比例是2/5,在任何大於5的5個連續自然數這個比例也是永恆的。第一級別的陰陽兩種上等數2/7,只要是連續7的自然數這個比例也是永恆的。由於上下兩等數的互相重疊,它們的比例是20/35,為什麼不是4/7,因為只有在大於7的連續35個自然數這個比例是不變的,如果連續7個自然數,它的比例有時是2/7,有時是3/7,有時是4/7.
其它級別也是一樣的。但如果這個級別的等數間隔距離是合數的,這個級別的等數都與前面級別的等數重疊的,所以這些級別就不用計算了。
這樣就立出以下的計算公式:
(6NN+6N)*3/5*5/7*9/11*11/13*......*(p-2)/p
(6NN+6N)是一個自然數的大體表達式,P《=N N以內最大的素數。
對應數段與同步區間
1、對應數段和精準的比例
計算一個級別的四種等數,只有在同一級別的對應數段為單位才是精準的比例,不然就有誤差。
一個N級別的標準單位是(6N+1)(6N-1);在計算N級別及以下的四種等數,它們的對應數段是N級別及以下的所有有性素數(不包括2和3的素數)的乘積。
對應數段的增大速度非常快。
對應數段的對應位置一定要在大於最大級別 的最小陰性等數。
在這位置以上任何連續的對應數段為單位的自然數中,它們的自己的等數是一定的,比例是精準的(不包括大於它的級別等數)。
2、與素數分布基本同步的SN區間
把自然數劃分成12,24,36……以12為遞增的一個個區間,這樣的區間叫SN區間。即:
12(1+2+3+……+N)-12(1+2+3+......+(N-1)=(6N^2+6N)-[6(N-1)^2+6(N-1)]=12N
SN區間與四種等數數列是同步的。
在這樣的區間內包括N級別及以下的所有四種等數數列的等數,並沒有比N級別大的數列等數,與四種等數的級別是完全同步的,所以與素數的分布也是同步的。
大於S8區間內都有8個以上的完全不等數
在每一個SN區間只有存在1至N級別的四種數列等數,每一級別等數的比例是可以確定,由於上下級別的滲透。就可以拿以下式來計算S8區間的完全不等數的至少個數。
12*8*11/35*95/143*251/323*479/575*779/899*1151/1295*1593/1763*2111/2303=8.2768
(由於計算的區間不是對應的標準單位,肯定會有誤差,為保險起見,把各級別中合數也給算上,一個級別中上下兩種等數的重疊則沒有算。)
其他每一個SN區間可用這種方法計算.
隨著區間的增大完全不等數計算的數量也會越來越多.以後都會超過8個.
誤差分析
在計算任何區間的等數,由於標準的比例與計算的區間都不能整除,所以存在誤差是一定,由於誤差掩蓋了等數的精準比例。
由於各個區間與相對應的標準單位不能同步,一個級別及以下的所有有性素數的乘積為這個級別的對應的標準單位,一個標準單位比對應的級別區間大得很多,如第一和第二兩個級別的標準單位就有5005,第二個N區間只有24,在5005的連續自然數中就有許多比第二級別大得多的等數,所以計算出的數值大多會有誤差。只有用標準的單位計算相對應的所有級別的等數才不會有誤差,由於標準單位的增速比等數級別快得多,所以就沒有所有等數級別的標準區間。
另外,可用最嚴格下取整的誤差分析方法,將SN區間捆綁成1,2,4,8,16......2^(N-1)的LN區間.在每一個大於S8的SN區間計算都大於8個完全不等數,在每一個LN區間都有2^N-1級別等數數列, 每級級別有4種等數數列,每一級別一種等數篩一次誤差極限是1 .每一個LN區間誤差極限是4*(2^N-1).
8*2^(N-1)-4*(2^N-1)=4
最嚴格下取整後大於L4的區間仍然還有4個完全不等數。
總結
根據以上的論證,在大於S8區間每一個SN區間都有8個以上的完全不等數.
嚴格的下取整後,大於L4的每一個LN區間都還有多於4個的完全不等數。
LN區間是無限多的,完全不等數與孿生素數對是一一對應的,所以孿生素數也是無限多的。
這個證明期待著權威的表態。
難題
哥德巴赫猜想
哥德巴赫猜想證明的困難在於,任何能找到的素數,在以下式中都是不成立的。2*3*5*7*。。。。。。*PN。。。。。。*P=PN+(2*3*5*7*。。。。。。*P-1)*PN前面的偶數減去任何一個素數PN的差必是合數.
在1742年給歐拉的信中哥德巴赫提出了以下猜想:任一大於2的整數都可寫成兩個質數之和。因現今數學界已經不使用“1也是素數”這個約定,原初猜想的現代陳述為:任一大於5的整數都可寫成三個質數之和。歐拉在回信中也提出另一等價版本,即任一大於2的偶數想陳述為歐拉的版本。把命題"任一充分大的偶數都可以表示成為一個素因子個數不超過a個的數與另一個素因子不超過b個的數之和"記作"a+b"。1966年陳景潤證明了"1+2"成立,即"任一充分大的偶數都可以表示成二個素數的和,或是一個素數和一個半素數的和"。 今日常見的猜想陳述為歐拉的版本,即任一大於2的偶數都可寫成兩個素數之和,亦稱為“強哥德巴赫猜想”或“關於偶數的哥德巴赫猜想”。
從關於偶數的哥德巴赫猜想,可推出任一大於7的奇數都可寫成三個質數之和的猜想。後者稱為“弱哥德巴赫猜想”或“關於奇數的哥德巴赫猜想”。
若關於偶數的哥德巴赫猜想是對的,則關於奇數的哥德巴赫猜想也會是對的。1937年時前蘇聯數學家維諾格拉多夫已經證明充分大的奇質數都能寫成三個質數的和,也稱為“哥德巴赫-維諾格拉朵夫定理”或“三素數定理”。2013年,秘魯數學家哈拉爾德·赫爾弗戈特在巴黎高等師範學院宣稱:證明了一個“弱哥德巴赫猜想”,即“任何一個大於7的奇數都能被表示成3個奇素數之和”。
黎曼猜想
黎曼猜想是關於黎曼ζ函式ζ(s)的零點分布的猜想,由數學家波恩哈德·黎曼(1826~1866)於1859年提出。德國數學家希爾伯特列出23個數學問題。其中第8問題中便有黎曼假設。素數在自然數中的分布並沒有簡單的規律。黎曼發現素數出現的頻率與黎曼ζ函式緊密相關。黎曼猜想提出:黎曼ζ函式ζ(s)非平凡零點(在此情況下是指s不為-2、-4、-6等點的值)的實數部份是1/2。即所有非平凡零點都應該位於直線1/2 + ti(“臨界線”(critical line))上。t為一實數,而i為虛數的基本單位。無人給出一個令人信服的關於黎曼猜想的合理證明。
在黎曼猜想的研究中,數學家們把複平面上 Re(s)=1/2 的直線稱為 critical line。 運用這一術語,黎曼猜想也可以表述為:黎曼ζ 函式的所有非平凡零點都位於 critical line 上。
黎曼猜想是黎曼在 1859 年提出的。在證明素數定理的過程中,黎曼提出了一個論斷:Zeta函式的零點都在直線Res(s) = 1/2上。他在作了一番努力而未能證明後便放棄了,因為這對他證明素數定理影響不大。但這一問題仍然未能解決,甚至於比此假設簡單的猜想也未能獲證。而函式論和解析數論中的很多問題都依賴於黎曼假設。在代數數論中的廣義黎曼假設更是影響深遠。若能證明黎曼假設,則可帶動許多問題的解決。
孿生質數
證明36N(N+1)+-1形孿生素數無限多。
36N(N+1)+-1形的孿生素數叫雁盪山孿生素數。如這種數對不是孿生素數的,它必有一邊或雙邊被小於它素數整除。
在這種數對中2和3不能整除它們,所以2和3不參加篩選;用5當篩子時,N是除以5餘2的所產生的陰性數(6n-1)能被5整除,N除以5餘1,3,4和0都不能被5整除;不管N除以5餘1.2.3.4.0,所產生的陽性數(6n+1)都不能被5整除,這樣所有的自然數中就有1/5被篩掉了。
用7當篩子時,N除以7餘2和4所產生的陽性數能被7整除,不管N除以7餘1.2.3.4.5.6.0,所產生的陰性數都不能被7整除。這樣就有2/7被篩掉了。
用11當篩子時,不管N除以11餘1.2.3.4.5.6.7.8.9.10.0,所產生的陰性數和陽性數都不能被11整除,11是一個無效篩子,不參加篩選。
總之,所有的素數在篩選N時有4種情況,一,不參加篩選。二,單一參加篩選的,如5,(5是唯一一個單一參予篩選的)。三,成對單邊參加篩選的。四,成對兩邊都參加篩選的。
N是無限多的,被5篩掉了1/5,剩下還是無限多的。再被7篩掉了2/7,剩下的還是無限多的。再一個個篩下去不管篩掉的是2/P還是4/P,剩下永遠是無限多的。
雁盪山孿生素數就是無限多的。
1849年,波林那克提出孿生質數猜想( the conjecture of twin primes),即猜測存在無窮多對孿生質數。猜想中的“ 孿生 質 數 ”是指一對質數,它們之間相差2。例如3和5,5和7,11和13,10,016,957和10,016,959等等都是孿生質數。
英國數學家戈弗雷·哈代和約翰·李特爾伍德曾提出一個“強孿生素數猜想”。這一猜想不僅提出孿生素數有無窮多對,而且還給出其漸近分布形式。2013年5月14日,《自然》(Nature)雜誌線上報導張益唐證明了“存在無窮多個之差小於7000萬的素數對”,這一研究隨即被認為在孿生素數猜想這一終極數論問題上取得了重大突破,甚至有人認為其對學界的影響將超過陳景潤的“1+2”證明。
36N(N+1)+ -1形的孿生素數,N《100000000 有109128對。
梅森質數
梅森素數的近似計算公式:
3*5/3.8*7/5.8*11/9.8*13/11.8*......*P/(P-1.2)-1=M
P是梅森數的指數,M是P以下的梅森素數的個數。
以下是計算的數值與實際數的情況:
指數5,計算2.947,實際3 ,誤差0.053;
指數7,計算3.764,實際4 ,誤差 0.236;
指數13,計算4.891,實際5,誤差0.109;
指數17,計算5.339,實際6,誤差0.661;
指數19,計算5.766,實際7,誤差1.234;
指數31,計算6.746,實際8,誤差1.254;
指數61,計算8.445,實際9,誤差0.555;
指數89,計算9.201,實際10,誤差0.799;
指數107,計算9.697,實際11,誤差1.303;
指數127,計算10.036 ,實際12,誤差1.964;
指數521,計算13.818,實際13,誤差-0.818;
指數607,計算14.259,實際14,誤差-0.259;
指數1279,計算16.306,實際15,誤差-1.306;
指數2203,計算17.573,實際16,誤差-1.573;
指數2281,計算17.941,實際17,誤差-0.941;
所有的奇素數都是準梅森數(2^N-1)的因 子數,則梅森合數的因子數是只有素數中的一部份。
在2^N-1的數列中,一個素數作為素因子第一次出現在指數N的數中,這個素數作為因子數在2^N-1數列中就以N為周期出現。在這種數列中指數是偶數的都等於3乘以四倍金字塔數。
在2^N-1數列中,指數大於6的,除梅森素數外,都有新增一個或一個以上的素數為因子數,新增的因子數減1能被這個指數整除。
一個梅森合數的因子數只有唯一一次出現在一個梅森合數中。
一個是梅森素數的素數,它永遠不是梅森合數的因子數。
一個是前面的梅森合數的因子數,它永遠不會是後面的梅森合數的因子數。
所有梅森合數的數因子減1都能被這個梅森合數的指數整除,商是偶數。
一個素數在不是梅森合數的準梅森數中第一次以因子數出現,這個素數減1能被這個準梅森數的指數整除,商不一定是偶數。
梅森素數都在[4^(1-1)+4^(2-1)+4^(3-1)+......+4^(n-1)]*6+1數列中,括符里種數暫叫四倍金字塔數。
凡是一個素數是四倍金字塔數的因子數,以後就不是梅森合數的因子數。
在4^(1-1)+4^(2-1)+4^(3-1)+......+4^(n-1)數列中的數,有不等於6NM+-(N+M)的數乘以6加上1都是梅森素數。
在2^P-1平方根以下的素數都以素因子在以前準梅森數中出現了,那這個梅森數必是梅森素數。但它的逆定理是不成立的。如果還沒有出現在以前的準梅森數中的素數,它也不定是梅森合數的因子數。
17世紀還有位法國數學家叫梅森,他曾經做過一個猜想:當2 -1 中的p是質數時,2 -1是質數。他驗算出:當p=2、3、5、7、17、19時,所得代數式的值都是質數,後來,歐拉證明p=31時,2 -1是質數。 p=2,3,5,7時,2 -1都是素數,但p=11時,所得2,047=23×89卻不是素數。
梅森去世250年後,美國數學家科爾證明,2 -1=193,707,721×761,838,257,287,是一個合數。這是第九個梅森數。20世紀,人們先後證明:第10個梅森數是質數,第11個梅森數是合數。質數排列得雜亂無章,也給人們尋找質數規律造成了困難。
迄今為止,人類僅發現49個梅森質數。美國中央密蘇里大學於2016年1月7日發現的質數,為迄今發現的最大質數,同時是一個梅森質數。由於這種質數珍奇而迷人,它被人們稱為“數學珍寶”。值得一提的是,中國數學家和語言學家周海中根據已知的梅森質數及其排列,巧妙地運用聯繫觀察法和不完全歸納法,於1992年正式提出了梅森素質分布的猜想,這一重要猜想被國際上稱為“周氏猜測”。
(GIMPS)項目於2016年1月7日找到人類已知的最大素數2 -1,該素數有22,338,618位,是第49個梅森素數。
2017年12月26日,美國田納西州日耳曼敦的GIMPS志願者喬納森·佩斯(JonathanPace)發現了第50個梅森素數277232917-1。這個超大素數有23249425位數,再次刷新了已知最大素數紀錄。

