簡史
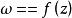 黎曼映射定理
黎曼映射定理黎曼在他1851年的博士論文中陳述了這個結果,但其證明不完整。康斯坦丁·卡拉西奧多里在1912年發表了第一個完整證明。該定理是複變函數幾何理論最基本、最重要的定理,是幾何函式論的基礎
定理
 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理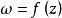 黎曼映射定理
黎曼映射定理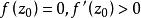 黎曼映射定理
黎曼映射定理(黎曼映射定理)若為單連通區域,其邊界多於一點,為中任意一點,則在上存在唯一的一個一個把意義對應地映射成單位圓內部的共形映射,且。
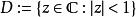 黎曼映射定理
黎曼映射定理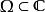 黎曼映射定理
黎曼映射定理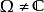 黎曼映射定理
黎曼映射定理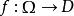 黎曼映射定理
黎曼映射定理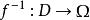 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理設 為開圓盤, 為單連通開子集。若 ,則存在一對一的全純映射,使 亦全純。換言之, 與 雙全純同構。
注意到二維的全純映射不外乎保持定向的共形映射,它保持角度與定向不變。
註記
 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理1)黎曼映射定理乃是存在性定理,一般無法具體表示從 至 的全純映射 。
 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理2)定理中對 的條件極寬鬆;舉例明之, 的邊界可能是碎形曲線,但 仍可透過共形映射映至單位圓盤,這在直觀上是很難想像的。
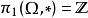 黎曼映射定理
黎曼映射定理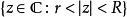 黎曼映射定理
黎曼映射定理3)此定理對 時即告失效:環型區域(形如 )之間的共形映射僅有反演、縮放與旋轉。
4)此定理在更高維度即不成立。
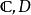 黎曼映射定理
黎曼映射定理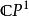 黎曼映射定理
黎曼映射定理5)在黎曼曲面的框架下,此定理可推廣為單值化定理:單連通黎曼曲面必同構於 或 。
證明
 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理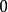 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理給定 和 ,我們希望構造一個函式 ,它把 映射到單位圓盤,把 映射到 。在這個證明概要中,我們假設 是有界的,且其邊界是光滑的,就像黎曼所做的那樣。記
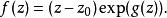 黎曼映射定理
黎曼映射定理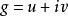 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理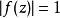 黎曼映射定理
黎曼映射定理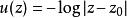 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理其中 是某個(待確定的)全純函式,其實數部分為 ,虛數部分為 。於是顯然 z是 f的唯一一個零點。我們要求對於 的邊界上的 有 ,因此我們需要在邊界上有 。由於 是全純函式的實數部分,我們知道 一定是一個調和函式,也就是說,它滿足拉普拉斯方程。
 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理 黎曼映射定理
黎曼映射定理於是問題變為:存在某個實值調和函式 ,對所有的 都有定義,且具有給定的邊界條件嗎?狄利克雷原理提供了肯定的答案。只要確立了 u的存在,全純函式的柯西-黎曼方程便允許了我們求出 (這個論證依賴於 是單連通的假設)。一旦構造了 和 ,我們還需要驗證所得到的函式 確實滿足所有需要的性質 。
相關知識
•黎曼曲面
•共形映射