簡介
特勒根定理適用於許多電路網路,只要該網路滿足總電流守恆(基爾霍夫電流定律(KCL))且所有閉合迴路電壓代數和為零(基爾霍夫電壓定律(KVL))。特勒根定理在分析電路和與電路相類似的複雜網路(如神經系統、代謝網路、管道網路與化工過程網路)中是一種常用的工具。
作用
套用特勒根定理可方便地證明電路中的互易定理、復功率平衡定理等。
特勒根定理1明確反映了電路實際功率的守恆。但特勒根定理2曾僅僅被認為只有功率守恆的數學形式,卻無法與實際電路對應,因此定理2也被稱為“擬功率定理” 。定理2後也被證明反映了電路實際功率的守恆 ,並具有共軛性。
定律
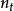 特勒根定理
特勒根定理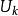 特勒根定理
特勒根定理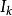 特勒根定理
特勒根定理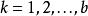 特勒根定理
特勒根定理現討論以圖G描述的一個有 b 條邊和個節點的網路。對於一個電路網路,邊表示二端元器件,節點處為元件間的電氣連線。對圖中所有邊設其兩端電勢差為,支路電流為()且均取關聯參考方向。若所有的迴路電壓均滿足KVL且節點電流都滿足KCL,則有:
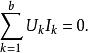 特勒根定理
特勒根定理特勒根定理的套用十分廣泛,適用於許多電路,無論其是否包含非線性元件、是否是穩恆電路。而且對電流電壓做線性變換不影響特勒根定理的成立,因為KCL與KVL不受線性變換影響。例如對電流電壓取平均時或拉普拉斯變換下特勒根定理仍然成立。特勒根定理的另一個常用推廣是對拓撲結構相同(關聯矩陣相同)的兩個不同網路的支路電壓和電流的積之和仍為零。即:
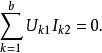 特勒根定理
特勒根定理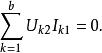 特勒根定理
特勒根定理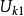 特勒根定理
特勒根定理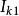 特勒根定理
特勒根定理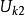 特勒根定理
特勒根定理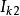 特勒根定理
特勒根定理式中、是第一個網路的電流電壓,、是第二個網路的電流電壓。特勒根原理的這一推廣可導出二連線埠網路的許多性質。
套用
許多物理系統都可以進行網路模擬以分析其動力學性質。特勒根定理對這些網路都適用,其中套用得最多的還是傳統的電路分析領域。特勒根定理在濾波器設計方面有廣泛的套用。
特勒根定理還可以套用於生化過程的研究。類似熱力學不可逆的動力學系統可以模擬為滿足基爾霍夫定律的電路,再運用特勒根定理來研究反應網路的拓撲結構(例如反應機理與代謝網路)。
特勒根定理亦可用於求複雜系統如化工廠和煉油廠的穩定性和最佳化方案。類似的有生產節點和物流鏈的過程系統均可用特勒根定理分析其生產與消費。