電路元件

一種主要對電路提供整流、開關和放大功能的（電路）元件。有源元件在電路中，也可以起到電阻和電容的作用，或者是將外部能量從一種形式轉化為另一種形式。例如：發光二極體、電晶體、半導體積體電路、光敏半導體器件和光發射半導體器件等。

電路元件

正文

電工中實際器件的數學模型。每一個電路元件的電壓u或電流i，或者電壓與電流之間的關係有著確定的規定。這種規定性充分地表達了這電路元件的特性。這種規定性也叫做元件約束。有時，在元件約束里也用到電荷q和磁鏈ψ，不過它們與電壓u和電流i總是滿足下面的關係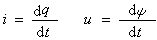

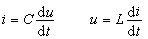
在電工理論中常取適當的元件，加以聯接來構造實際器件或電路的模型，以便於分析計算。表中列出了一些常見的電路元件和它們的元件約束。表中，除了獨立電壓源和獨立電流源之外，如果元件參數是常數，對應的元件叫做定常元件。定常電容器和定常電感器的元件約束分別是

式中C和L是常數
電路元件通常分為時變元件與時不變元件、線性元件與非線性元件、分布參數元件與集總參數元件。
時變元件與時不變元件　如果元件參數是時間 t的函式，對應的元件叫做時變元件；否則叫做時不變元件。定常元件是一種時不變元件。時變元件的一個例子是用手或某種機構不斷地反覆轉動電位器的軸，電位器的電阻就隨時間變化。這時可以用時變電阻器作為電位器的模型。例如設電阻R是R＝1000(1＋0.6sint)歐，則時變電阻器的元件約束是

u =Ri=【1000(1+0.6sint)】i

線性元件與非線性元件　如果元件參數是電壓 u或電流i的函式(有時也可以是電荷q或磁鏈 ψ的函式)，對應的元件叫做非線性元件;否則叫做線性元件。 定常元件是一種線性元件。非線性元件的一個例子如下：半導體二極體的數學模型為

i=a(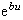－1)(a>0,b>0)

上式為元件約束。它在電流i與電壓u之間規定了一個代數關係，元件是非線性電阻器。電阻R 是

上式說明，電阻R 是元件電壓u的函式。
分布參數元件與集總參數元件　一個實際電工器件，在不同條件下可以有不同的電路模型。例如一根金屬導線，當其中電流的頻率很低時，可以用定常電阻器作為它的模型。當導線中電流的頻率很高時，導線中各處的電流並不相等，也就是說導線中的電流和空間位置有關。圖1表明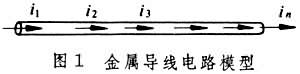，在不同的空間位置上,電流i1，i2，i3……一般地互不相等,特別是流入導線一端的電流i1不必等於從導線另一端流出的電流in。
對於某個電工器件，凡是要考慮其電流、電壓和空間位置或者說要考慮其電流、電壓在空間的分布情況時，即為分布參數元件，必須採用具有分布參數的模型。均勻傳輸線就是一種典型的分布參數電路。不考慮電流、電壓在空間分布的模型，叫做集總參數模型。表中所列電路元件都是集總參數元件或稱集總元件。

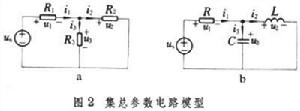電路元件

由集總參數元件組成的電路稱為集總參數電路或集總電路。在這種電路里，電流、電壓除了在元件上應滿足元件約束之外，還要滿足基爾霍夫定律。
對於圖2a所示的集總參數電路，可以寫出以下電路方程。
基爾霍夫第一定律方程：

i1＝i2＋i3

基爾霍夫第二定律方程：

u1＋u2＝us　u2＝u3

元件約束方程：

u1＝R1i1　u2＝R2i2　u3＝R3i3　us＝f(t)

這個電路的電路方程是一組代數方程。如果電路中還含有受控電源、理想變換器、運算放大器等元件，列出的電路方程仍然是一組代數方程。因為聯繫這些元件的電壓和電流的元件約束是代數關係,不含對時間t的導數（如表<所示）。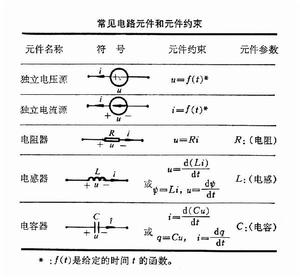

電路元件

對於圖2b電路，它的基爾霍夫定律方程和圖2a電路的相同。若圖的R、L、C是常數，即對應的元件是定常元件，則元件約束是： u1＝Ri1 　 us＝f(t) 由於電路里含有電容元件和電感元件，電路方程里有對時間t的導數。
假設已知獨立電壓源的電壓的時間變化即已知f(t)，已知圖a 中三個定常電阻器的常值參數R1、R2、R3,或已知圖b中三個定常元件的常值參數R、L、C,根據非齊次線性代數方程的理論或非齊次線性常係數常微分方程的理論，從原則上講可以求解圖a、圖b各處的電流和電壓。獨立電壓源的電壓us以及獨立電流源的電流is常稱為激勵，而其他的電流、電壓叫做回響。
當電路元件是時變的或者是非線性的，甚至既是時變、又是非線性的，求解電路方程很困難。一般需用計算機來解複雜的電路方程。

配圖

相關連線