從電阻電路的分析中,我們可以循到線性電阻電路分析的一些規律,可以將其當做一般性定理來使用。利用電路定理將複雜電路化簡或將電路的局部用簡單電路等效替代,以使電路的計算得到簡化。電路定理分別包括:①、疊加定理;②、替代定理;③、戴維南定理(諾頓定理);④、及最大傳輸定理;⑤、特勒根定理;⑥、互易定理;⑦、對偶原理。
一.定理陳述及其解釋性證明
1.定理陳述:在線性電路中,任一支路的電流或電壓是電路中各個獨立源分別作用時在該支路中產生的電流或電壓的代數和。
2.定理證明:
分析圖中Ua、I1與各個激勵的關係
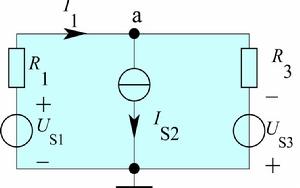 電路定理
電路定理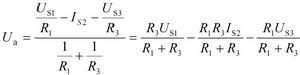 電路定理
電路定理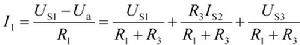 電路定理
電路定理US1單獨作用時(IS不作用時開路,US不作用時短路):
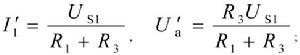 電路定理
電路定理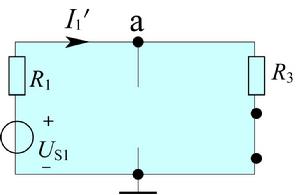 電路定理
電路定理IS2單獨作用時(US不作用時短路):
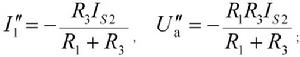 電路定理
電路定理 電路定理
電路定理Us3單獨作用時(IS不作用時開路):
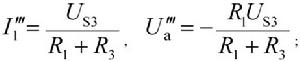 電路定理
電路定理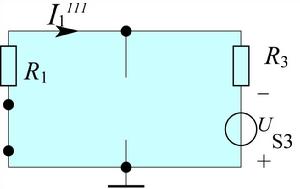
顯然有:
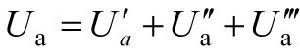 電路定理
電路定理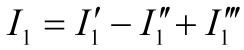 電路定理
電路定理3.解釋性證明:
線性電路獨立變數方程是線性代數方程,其方程右端項與各電源成正比,
∴由克萊姆法則知獨立變數與各電源成正比,且再由支路VAR知各支路u、i亦與各電源成正比。
4.使用疊加定理的注意點
(1)、疊加定理是線性電路疊加特性的概括表征,其重要性不僅僅在於可用疊加法分析電路本身(往往在電源分別作用時構成簡單電路時才用疊加法分析),更重要的是在於它為線性電路的定性分析和一些具體的計算方法提供了理論依據。
(2)、若uS不作用,則短接之,若iS不作用,則開路之;而受控源不是激勵,即作圖分解時受控源始終保留在電路中,此外,定理中“各個獨立源”可換為“各組獨立源”(分組疊加)。
(3)、只適用於線性電路中求解電壓與電流回響,而不能用來計算功率。這是由於只有線性電路中的電壓或電流才是激勵的一次函式,而功率與激勵不再是一次函式關係。
(4)、求“代數和”時要注意各電壓或電流的參考方向
(5)、該定理可理解為:線性電路的回響與各激勵成正比。如里上例電路:Ua=K1US1 K2IS2 K3US3特別地,當線性電路只有一個激勵時,則激勵擴大K倍,任意支路的回響(電壓或電流)也擴大K倍。這稱為線性電路的齊次性。實際上:線性性質包括疊加性(可加性)和齊次性(比例性,均勻性).
替代定理(置換定理)