定義
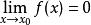 無窮小量
無窮小量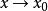 無窮小量
無窮小量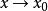 無窮小量
無窮小量無窮小是極限為零的函式。如是自變數,因變數極限為零的函式。此時f(x)就是的無窮小。
無窮大是指絕對值大於任何數的函式,因此負無窮不是無窮小,而是無窮大。
 無窮小量
無窮小量設f在某x的空心鄰域有定義。
 無窮小量
無窮小量 無窮小量
無窮小量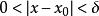 無窮小量
無窮小量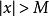 無窮小量
無窮小量 無窮小量
無窮小量 無窮小量
無窮小量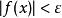 無窮小量
無窮小量 無窮小量
無窮小量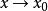 無窮小量
無窮小量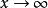 無窮小量
無窮小量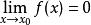 無窮小量
無窮小量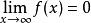 無窮小量
無窮小量對於任給的正數 ε(無論它多么小),總存在正數 (或正數 )使得不等式(或 )的一切 對應的函式值 都滿足不等式 ,則稱函式 為當 (或 )時的無窮小量。記做: (或 )。
性質
1、無窮小量不是一個數,它是一個變數。
2、零可以作為無窮小量的唯一一個常量。
3、無窮小量與自變數的趨勢相關。
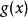 無窮小量
無窮小量 無窮小量
無窮小量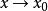 無窮小量
無窮小量4、若函式 在某 的空心鄰域內有界,則稱g為當 時的有界量。
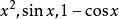 無窮小量
無窮小量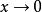 無窮小量
無窮小量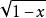 無窮小量
無窮小量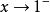 無窮小量
無窮小量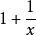 無窮小量
無窮小量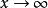 無窮小量
無窮小量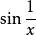 無窮小量
無窮小量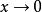 無窮小量
無窮小量例如 ,都是當 時的無窮小量, 是當 時的無窮小量,而 為 時的有界量, 是當 時的有界量。特別的,任何無窮小量也必定是有界量。
5、有限個無窮小量之和仍是無窮小量。
6、有限個無窮小量之積仍是無窮小量。
7、有界函式與無窮小量之積為無窮小量。
8、特別地,常數和無窮小量的乘積也為無窮小量。
9、恆不為零的無窮小量的倒數為無窮大,無窮大的倒數為無窮小。
無窮大
 無窮小量
無窮小量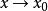 無窮小量
無窮小量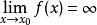 無窮小量
無窮小量當自變數x趨於x時,函式的絕對值無限增大,則稱 為當 時的無窮大。記作 。
同樣,無窮大不是一個具體的數字,而是一個無限發展的趨勢。
階的比較
前提條件
無窮小量是以0為極限的函式,而不同的無窮小量收斂於0的速度有快有慢。因此兩個無窮小量之間又分為高階無窮小 ,低階無窮小,同階無窮小,等價無窮小。
 無窮小量
無窮小量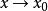 無窮小量
無窮小量 無窮小量
無窮小量 無窮小量
無窮小量首先規定 都為 時的無窮小, 在某 的空心鄰域恆不為0。
高低階無窮小量
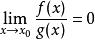 無窮小量
無窮小量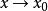 無窮小量
無窮小量,則稱當 時,f為g的高階無窮小量,或稱g為f的低階無窮小量。
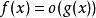 無窮小量
無窮小量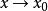 無窮小量
無窮小量記做 ( )
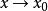 無窮小量
無窮小量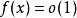 無窮小量
無窮小量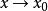 無窮小量
無窮小量特別的,f為當 時的無窮小量記作 ( )。
同階無窮小量
 無窮小量
無窮小量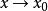 無窮小量
無窮小量當 (c≠0)時,ƒ和ɡ為 時的同階無窮小量。
當x→0時的同階無窮小量:
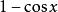 無窮小量
無窮小量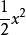 無窮小量
無窮小量與
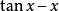 無窮小量
無窮小量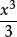 無窮小量
無窮小量與
等價無窮小量
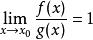 無窮小量
無窮小量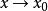 無窮小量
無窮小量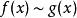 無窮小量
無窮小量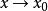 無窮小量
無窮小量,則稱ƒ和ɡ是當 時的等價無窮小量,記做: ( )。
等價無窮小量套用最廣泛,常見的有:
當x→0時
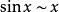 無窮小量
無窮小量 無窮小量
無窮小量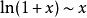 無窮小量
無窮小量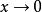 無窮小量
無窮小量, , ( )

