簡介
 虛數
虛數【虛數】:在數學上用i表示,且規定i的平方等於-1
【虛時間】:用虛數測量的時間。
廣義
在廣義相對論中,由於時間和空間在公式中表達的方式,使實際談論時間的創生成為可能。麻煩的是,在經典理論中,當空間和時間“開始形成”時,實在的點本身是數學中的奇點,數學失效了,所以它不能給你一個創生論。你在傳統的宇宙論中所能說的是,存在許多不同的可能宇宙,它們所有都和愛因斯坦方程式相符合。我們恰巧在這個宇宙中生活的事實,毋寧說純粹是出於偶然。你不能賦予任何理由——甚至在原則上也不能。你所能說的一切是條件陳述:假定宇宙在這一時刻處在這個狀態,則它在以後的時刻將處於那個狀態。它是條件性類型的演化。可能性
然而,當你談到虛時間,就有一個奇怪的可能性,也就是“現在”不一定要有一連串的過去時刻。如果我們從現在這一時刻往過去回溯,在很長的時間內一切都完全正常地進行,甚至在虛時間中也是如此。只要你使用這個唯象的時間,看起來就像你在通常時間裡回溯過去。但是隨著你往以前退去,越來越接近傳統的實時間圖像中變成原點之處,你就發現時間的性質在改變,復的或虛的變得越來越有份量。最後,在經典理論中應該是奇點的東西被抹平了,你就得到這張漂亮的圖畫,這些碗狀的宇宙創生圖像。那裡沒有起點,只是某種光滑的形狀。
虛的含義
虛時間中的詞“虛”不是指想像:它是指數學中非常古老的觀念。對於一位給定的觀察者,空間和時間當然是可區分的:我們用尺來測量空間,用鐘錶測量時間。愛因斯坦和赫爾曼·閔可夫斯基在上世紀初指出,不同的觀察者的空間和時間概念,只不過是同一個統一的空間——時間觀念的不同方面。空間——時間是四維空間幾何,它有某些類空間的方向和某些類時間的方向。所以就一定意義上來講,在那裡空間和時間概念仍是可以區分的。奇點
是什麼
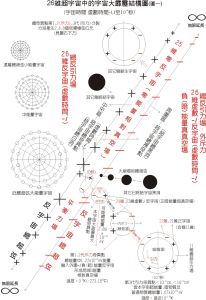
 虛時間包圍之奇點-模型圖
虛時間包圍之奇點-模型圖 在通常黑洞的中心存在著奇點,在鏇轉黑洞的赤道上存在著環狀的奇點。在介紹黑洞、大爆炸、大塌縮的讀物里,“奇點”這個陌生的名詞頻頻出現。既彆扭又難懂,難道就找不到其它的表達方法嗎?讀者們大概都有這樣的抱怨。
但是,我們只能原樣照搬地使用這個數學名詞。所謂奇點,淺顯易懂地說(也許筆者的解釋並不淺顯易懂),是一個非常奇特的點,它存在於黑洞中以及大爆炸的起始點、大塌縮的終結點。
前面講過,在數學上當分數的分子為有限值,而分母變成零時,或者三角函數裡的正切函式tanx當x成為90度時的值都是無窮大。當x從89度開始漸漸接近90度時,tanx的值就無限地接近正無窮大;反過來當x從91度開始一點點地變小接近90度時,函式值將無限地接近負無窮大;當x正好是90度時,函式值(的絕對值)為無限大,無法判定其正負。數學上的奇點就是如此奇妙的點。
雖然簡單地使用了無窮大,但是筆者個人認為這樣的數在物理學裡是不存在的……人們為了進行加減乘除開平方等各種數學計算,引入了分數、無理數、負數等等,但是無論什麼數都不許被零除,在每一所學校里教師都這樣嚴格地教導學生。無窮大只是嘴上說說而已,實際中從不使用。比如:我們說宇宙的大小為150億光年,儘管極為廣闊,但絕不是無窮大。
筆者認為,把數學套用到物理的現實世界時,所謂無窮大的數只是不得已而暴露出的不真實的數值。儘管是不真實的數值,如果它能夠給我們帶來方便的話,用之也無妨。
下面舉個簡單的例子。在物理問題中經常出現‘有個質量為m的點’之類的用詞,質點是為了把力學問題簡化而構想的非現實的點狀物體,常有腦子好用且愛鑽牛角尖的學生提出‘那個質點的密度是多大?’的問題,令教師為難,最合適的回答也許是‘不考慮質點的密度’。事實上正是因為所處理的問題不涉及密度,我們才放心地把‘質點’的概念引入力學之中。
在物理學裡,對於(認真去分析的話)很奇怪的概念,只要我們不是直接地研究它,通常都採取默認的態度,這樣的事例很多。當其影響不可避免時,則重新修正我們的思考方式。質點是力學中的約定俗成的概念。當我們分析發生在時空中的電子-光子相互作用時,也會出現剛才說過的無窮大的困難,該困難至今仍未得到完美的解決(或理解)。
是否存在
接下來我們要討論的問題是霍金等人指出的宇宙的奇點。對於不帶自轉的黑洞來說,視界或者說史瓦西半徑以內的任何物質(包括光)都不可能跑出來,它們都落向中心點。黑洞大概是密度極高的球狀物體……我們很願意這樣去想像,但它也可能是由中子星進一步縮聚而成,仍然保持著天體的形狀。總之,黑洞的形狀無人知曉。原因在於,誰也無法知道黑洞之中究竟是什麼狀態。從它的外面來想像,我們只知道中心的引力值是無窮大,所以不妨認為黑洞內部的質量全部集中在中心點上。由於引力強的地方空間彎曲得也厲害,隨著接近中心,彎曲程度也愈來愈激烈。假如在不帶自轉的正球形黑洞裡,空間將一下子靠向中央(那裡的情景很難打比方,也很難想像),並且急劇地彎曲起來。在任何曲線的任何部位上,只要取無限短的一小段,都可以將其視為某個圓弧的一部分,圓的半徑越小,曲線在該處的彎曲程度就越大。我們乘火車時,在轉彎處的鐵路旁邊經常能夠看到標有轉彎半徑的標記,列車的設計時速越高,所要求的最小轉彎半徑就越大。我們將半徑的倒數(1除以半徑)叫做曲率,曲率越大,曲線越彎曲。
舉例

哈特爾和霍金的發現
彭羅斯和霍金以前的理論研究認為:宇宙始於大爆炸終於大塌縮,即宇宙從奇點創生並且終結於奇點。在奇點處物理定律失效,所以有關初始及終結的問題被排除到了物理定律的適用範圍之外,但是對於從不迴避實際問題的科學家來說,在感情上不能容忍奇點這樣的超現實的東西。在數學上碰到奇點時,總是想方設法繞道而行,換句話說,絕對不承認分母為零的事情。大家可以從稍後的介紹看出,霍金的思想正是如此。霍金為了調查宇宙從大爆炸到大塌縮的路徑,使用了一種特別的數學手段——路徑積分。最先使用這種方法的人是擅長用畫圖的手段求解物理問題的美國物理學家理察·費曼,他與朝永振一郎、施溫格共同獲得了1965年度諾貝爾物理學獎。當時朝永與施溫格用數學公式完成了量子電動力學的理論體系,費曼用方便易懂的圖解方法(橫軸為空間,縱軸為時間)進行了同樣的工作。費曼圖被廣泛運用於物理學的各種領域,它表示了研究對象怎樣從過去演變到未來,例如電子放出或吸收光子的過程,費曼用直觀的視覺反映了自己的研究。因此,某個物體從A地點(或狀態)過渡到B地點(或狀態)時,其中過程是怎樣變化的即沿哪一條路行進的呢?費曼擅長用圖研究這類問題。大家可能感到路徑積分是先通過圖進行分析然後再把分析過程數學公式化的方法。路徑積分已經成為理論物理學的最重要的手段之一。實際上,有關路徑積分的計算是非常繁瑣的,例如時間積分就有無限多種組合方法。下面的例子也許不一定適當,為了便於理解還是請大家一起來看一下。路徑積分指出光的路線
 虛時間
虛時間哈特爾發現
哈特爾和霍金所發現的是:如果你假設,宇宙在虛時間裡的過去歷史圖像是所有可能的、恰好和我們現在時刻宇宙相符的這類形狀,而你多多少少用傳統量子力學方式來解釋之,至少在原則上你會得到整個宇宙唯一的波函式。對這個發現的分析
這樣,你就得到了這個沒有過去的美妙圖畫,宇宙根本不從任何東西產生出來。因為它是一個自洽的數學結構,所有你真正能說的是宇宙存在。和從某點創生宇宙的圖景不一樣,這宇宙沒有過去,因為沒有任何它在其中創生的東西。如此,宇宙從“無”中創生的說法,實際上有一點用詞不當;這是辭彙“無”的誤用。它不只是指在空虛的空間中出現宇宙,你也許可以把這空間稱為“無”:因為甚至連創生事件也不存在,所以根本不存在任何東西!
在這些理論中,動詞過去時態的使用變成不恰當。當然,在人們相信實時間時就建立了時態。不幸的是,我們還沒有在虛時間中表示時態的語言形式。因此,在這層意義上,說“從無中創生”肯定是誤導的。它對於這個在預先存在的時間中忽然出現的宇宙圖像很合適,可是它並不是哈特爾——霍金態的貼切描述。
為了預言宇宙是如何起始的,人們需要在時間開端處也能成立的定律。在實時間內只存在兩種可能性:或者時間往過去回溯直至無窮,或者時間在一個奇點處有一個開端。人們可以把實時間認為是從大爆炸起到大擠壓止的一根直線。但是,人們還可以考慮和實時間成直角的另一個時間方向。這叫做時間的虛方向。在時間的虛方向,不必要任何形成宇宙開端或終結的奇點。
在虛時間裡,沒有科學定律在該處失效的奇點,也沒有人們需要在該處乞求上帝的宇宙邊緣。宇宙既不創生也不毀滅結束。它就是存在。
也許虛時間才真正是真實的時間,而我們稱為實時間的僅是我們的想像。宇宙在實時間裡各有一個開端和終結。可是在虛時間裡,不存在奇點或邊界。因此,也許我們稱為的虛時間是真正更基本的,而我們叫做實時間的,只不過是我們發明的觀念,用來幫助自己描述我們認為的宇宙的樣子。
許多人相信,上帝允許宇宙按照一套定律來演化,上帝並不干涉演化的過程促使宇宙觸犯這些定律。然而,仍然需要靠上帝去卷緊發條並選擇如何去啟動它。只要宇宙有一個開端,我們就可以構想有一位造物主。但是,如果宇宙確實是完全自足的,那還會有造物主的存身之處嗎?
宇宙如何終結
宇宙如何終結存在兩種基本理論。一種是開放宇宙的觀念,它會繼續演化,不會突然終止;事情僅僅是緩慢下來,並且按照熱力學第二定律到達熱死。另外一種是閉合宇宙的觀念,它會停止膨脹,而且會向自身坍縮回來,這有時被稱作大擠壓,像是大爆炸,只不過在時間上顛倒過來就是了。最簡單的理論
儘管那種觀念具有巨大威力,在統一這些概念方面仍然可以走得更遠些。如果你用虛數來測量時間方向,那你就得到了空間和時間之間的完全對稱,這在數學上是非常美妙和自然的觀念。無邊界構想就是利用這個數學的單純化,導致所有可能的宇宙的初始條件中的最簡單的理論。但是,人們不應認為日常經驗中可以直接體驗到虛時間。它是一種用來表達物理方程式的美麗的數學觀念,同時在此情形下,它是一個解釋宇宙初始狀況的特殊構想。
霍金的奇性定理
霍金的奇性定理指出,愛因斯坦的廣義相對論和一定的觀測相結合,意味著宇宙在開端處必須有一個奇點。如果你向時間過去回溯,到達某一點就不能再過去了。我們通常將此視為時間的起點。這擾亂了許多假定宇宙為無限古老的人。霍金的思想指出宇宙有一個開端,有人覺得,這符合創世紀所描述的宇宙在時間中創生;雖然其他神學家說,上帝創世並不見得就發生在我們的時間裡。
上帝也許可以創生一個無限宇宙,但是霍金的思想隱含著時間有一個開端。現在,我們當然知道,愛因斯坦理論在非常接近於那個開端處不能成立。所以我們知道,該理論本身在那裡失效。那就引起了這樣的可能性:即也許宇宙是無限古老的,或者也許是別的什麼樣子的。
現在許多人連霍金都覺得時間概念本身在接近開端處失效,因此談論開端之前是什麼並沒有意義:在此之前是否有無限的時間呢?還是只有有限的時間?宇宙是否有一個時間上的絕對開端呢?由於時間觀念本身在這些極早的時刻並沒有多少意義,所以那些問題有些是沒有什麼意義的。我們能肯定的是,就我們所知,時間有一個開端,可是這開端有一個點,一旦超過那一點,我們標準的時間概念就失效。
在哈特爾——霍金的無邊界構想中,宇宙開端的方式是:時間的行為非常滑稽:在技術意義上時間是虛的。這樣時間沒有邊緣,你似乎有一個地球的表面。譬如說你從北極出發,沿著經線往外走。這些經線的確從北極散開,北極是完全規則的。
這就是霍金的宇宙圖像:這個虛時間既沒有開端也沒有終結。它沒有必要永遠前進。它是有限的,如同地球只有有限的面積一樣。在地球上不可能永遠繼續向北走下去。由於你可以走到最北的一點,在某種意義上,你會走到盡頭。但在另一種意義上,在那裡並沒有真正的終點。
因此,霍金說,宇宙在開端處沒有邊界,所以宇宙是一個自足的整體。他還論斷道,上帝實在沒有必要去啟動宇宙:宇宙能夠自身存在那裡,不需要上帝去創造它。
是否有造物主
還會有造物主的存身之處嗎?上帝是否創造宇宙的問題和宇宙是否有邊緣並沒有直接關聯,儘管許多人認為是相關的。它們實際上是不怎么相干的。例如,我在一張紙上畫了兩條線。這條直線有兩個端點:如果我想像時間以那種方式前進的話,則你可把這一個端點稱為起點,那一個端點稱為終點。如果時間沿相反方向前進,則情況就變相反,這一個端點稱為終點,那一個端點稱為起點。你可將此當成宇宙的一個模型,一個具有開端和終結的宇宙。
這個圓圈表示另一個宇宙。當時間前進時,在某種意義上存在一個最早的時刻;可是如果你沿著這圓圈的線,該線沒有終點,它只是不斷圍繞著。
但是,我自己畫了這些線,所以在某種意義上而言,我創造了它們。但是它們是否有開端或終結,對我是否創造了它們的問題毫無影響。
我認為宇宙的情形是類似的。在霍金的舊模型中,宇宙具有一個開端,也許還有一個終結。新模型更像這沒有開端和終結的圓圈。在某種意義上它有個最左的端點;這樣你能說有某種像是最早時刻和最晚時刻的東西。但是,就更技術性的意義來說,既不存在開端也不存在終結。而且這兩種都可以由上帝來創造。我們必須先有信仰,才能問它是否由上帝創造的問題。這是科學既不能證實也不能證偽的事體。
我想,霍金在他的書中小心避免公開直截了當地說沒有上帝。他僅說:還會有造物主的存身之處嗎?然而我想他希望人們從這裡得出何種結論是十分明顯的。
霍金觀點
 虛時間
虛時間這些奇怪的概念都是愛因斯坦的廣義相對論的必然推論,使人感到很無奈。但是,霍金並沒有因此放棄努力,他把量子理論用到路徑積分里發展了原來的路徑積分方法,提出了‘無境界’宇宙模型。霍金勇敢地否定了自己以前提出的奇點定理,找出了迴避奇點這個數學疑難的方法。
不過,無境界宇宙也不是個一提就懂的概念。雖然時空不可分割,為了便於理解,這裡只考慮時間,所謂無境界就是沒有任何斷頭的意思,霍金的結論用另一種說法來說就是:任何時候都存在時間,即使在大爆炸之前或大塌縮之後也不例外。
霍金的宇宙模型是個象地球一樣的球形,球的表面代表宇宙空間,北極點對應於大爆炸。宇宙從北極點開始,球的緯度對應於宇宙的大小,隨著時間的推移,宇宙逐漸沿北緯80度圈、70度圈、60度圈……的方向擴大,現在是宇宙誕生後大約150億年,大致相當於北緯40度附近,再過100億年左右宇宙將膨脹到最大狀態——赤道上,然後轉入收縮,進入地球模型上的南半球,最後是大塌縮,即模型上的南極點。
用地球來打比方是為了便於大家理解,重要的是:不把北極點和南極點當作特殊的點。的確,從幾何學的角度看,極點與表面的其它部分完全相同。當然,地球的南、北極是自轉的軸,按照緯度的定義,它們分別對應於南、北90度。霍金的宇宙模型里的南北極沒有任何特殊的構造。
霍金與哈特爾一起消除了大爆炸和大塌縮的宇宙奇點,用地球來比喻他們的模型再恰當不過了,無論是在北極還是在南極都不存在無窮大或者其它的特殊因素。
愛因斯坦觀點
虛時間是一具很難掌握的概念,它可能是我的書的讀者覺得最困難的東西。我還由於使用虛時間而受到哲學家們猛烈的批評。虛時間和實在的宇宙怎么會相乾呢?我以為這些哲學家沒有從歷史吸取教訓。人們曾經一度認為地球是平坦的以及太陽繞著地球轉動,然而從哥白尼和伽利略時代開始,我們就得調整適應這種觀念,即地球是圓形的而且它繞著太陽公轉。類似的,長期以來對於每位觀測者時間以相同速率流逝似乎是顯而易見的,但是從愛因斯坦時代開始,我們就得接受,對於不同的觀測者時間流逝的速率不同。此外,宇宙具有唯一的歷史似乎是顯然的,但是從發現量子力學起,我們就必須把宇宙考慮成具有任何可能的歷史。我要提出,虛時間的觀念也將是我們必須接受的某種東西。它和相信世界是圓的是同等程度的一個智慧的飛躍。在有教養的世界中平坦地球的信仰者已是鳳毛麟角。
你可以把通常的實的時間當成一根從左至右的水平線。左邊代表早先,右邊代表以後。但是你還可以考慮時間的另一個方向,也就是書頁的上方和下方。這就是時間的所謂的庶的方向,它和實時間夾直角。
引入虛時間的緣由是什麼呢?人們為什麼不只拘泥於我們理解的通常的實時間呢?正如早先所提到的,其原因是物質和能量要使時空向其自身彎曲。在實時間方向,這就不可避免地導致奇性。時空在這裡到達盡頭。物理學方程在奇點處無法定義,這樣人們就不能預言會發生什麼。但是虛時間方向和實時間成直角。這表明它的行為和在空間中運動的三個方向相類似。宇宙中特質引起的時空曲率就使三個空間方向和這個虛的時間方向繞到後面再相遇到一起。它們會有任何可以叫做開端或者終結的點,正和地球的表面沒有開端或者終結一樣。
1983年詹姆·哈特爾和我提出,對於宇宙不能取在實時間中的歷史求和,相反的,它應當取在虛時間內的歷史的求和,而且這些歷史,正如地球的表面那樣,自身必須是閉合的。因為這些歷史不具有任何奇性或者任何開端或終結,在它們中發生的什麼可完全由物理定律所確定。這表明在虛時間中發生的東西可被計算出來。而如果你知道宇宙在虛時間裡的歷史,你就能計算出它在實時間裡如何行為。以這種方法,你可望得到一個完整的統一理論,它能預言宇宙中的一切。愛因斯坦把他的晚年獻身於尋求這樣的一種理論。因為他不相信量子力學,所以他沒有尋找到。他不準備承認宇宙可以有許多不同的歷史,正如在對歷史求和中的那樣。對於宇宙我們仍然不知道如何正確地對歷史求和,但是我們能夠相當肯定,它將牽涉到虛時間以及時空向自身閉合的思想。我認為,對於下一代的人而言,這些思想將會像世界是圓形的那么自然。虛時間已經成為科學幻想的老生常談。但是它不僅是科學幻想或者數學技巧。它是某種使我們生活於其中的宇宙成形的某種東西。
其他觀點
不曾存在的東西
 虛時間
虛時間把不曾有的數當做仿佛真的存在一樣地去研究,這樣做未嘗不可以。
我們再多舉些數學味道更濃的例子,比如arcsins(正弦值為5的角的數’。引入i的概念以後,對arcsin5之類的怪數也可以進行計算與分析,只要容忍i,就可以對其它的怪數置之不理,進行漂亮的數學處理。我們是不是對i太遷就了呢?
筆者建議對數學感興趣的讀者思索一下這個問題。如果您認為它不公平的話,就請您自己消除這種不公,創造一門新的數學分支。
只將虛數i數學系統化是有其充分理由的,複數可以適用於從加減乘除四則運算到微分積分的各個數學領域,‘可以不矛盾地數學系統化’。 3+2i與5-4i的和是8-2i,其它的演算也一樣沒有問題。雖說從現實觀點看,初始的i本身是個奇妙的數字,但只要承認它的存在,其它方面就可以萬事大吉。
有點象非歐幾何的情形:只要承認‘通過一點可以畫出一條直線及其平行線’的非歐幾里德公理,就不會遇到其它的矛盾。不過非歐幾何可以套用於球面,它具有實際的意義。問題是其它的數學計算無法進行,如果對於除了i以外的其它不存在的數,數學法則也能夠成立的話,數學家們應該早就把它形式化了。 所以人們引入了叫做i的虛數,它冠冕堂皇地進入了教材並成為數學家的研究對象。
實數就是一切
數學是以公理為基礎、沒有矛盾地拓展的理論,而物理學則是以自然界為研究對象的學問。由於物理學中常常定量地分析事物,所以大量地借用了數學家們所設定的數及其演算規律。不過,物理學家從未向數學家支付過專利費(或使用費),因為數學的發展很大程度上依賴於物理學的需要,兩門學科相輔相成。現在的問題是,物理學怎樣看待虛數i。
長度是最單純、最直觀的物理量之一,為了表達長度,人們定義了基本單位——1米,因此有了物體的長度為7米、0.8米等說法。32千米也罷、2.734米也罷,各種長度都有它的表達方法。
物理學的研究對象和實數之間(借用數學家的話邊長為1米的正方形,它的對角線長度約為1.414米,純粹派的人士度、質量等各種量,只要定義其單位,然後使用數字就能正確地表達量的物理學的研究對象和實數之間(借用數學家的話)是一一對應的關係,用全部實數能夠完全地記述自然界,從這個意義上說,在物理學裡不應該有虛數或複數的市場。)是一一對應的關係,用全部實數能夠完全地記述自然界,從這個意義上說,在物理學裡不應該有虛數或複數的市場。
不錯,在交流電理論中確實運用了複變函數,但那只不過是為了圖方便,如果你不嫌煩的話,運用正弦、餘弦等實函式也完全可以解決問題。
從現實問題出發很難理解複數(特別是一部分為虛數)所表示的量。我們很容易理解3個蘋果的意思,當別人向你要3i個蘋果時怎么辦?毫無辦法!教室的黑板到對面牆壁的距離是12i米、這箱桔子重4i千克之類的話,誰也沒有聽說過。
大爆炸之前
假設
如果將宇宙比作地球的話,最初的大爆炸就相當於北極點,請讀者容忍一下接受這個說法。霍金在使用路徑積分法的同時把時間虛數化(關於虛數我們將在下一小節詳細介紹)從而化解了時間的境界。各位一定會問,這到底是怎么回事?用地球作比喻的話,大爆炸以前的宇宙對應於哪個部位呢?難道存在比北極點更‘北’的地方嗎?結果
答案是,用路徑積分法確實能夠使時間的境界消失,由於大爆炸以前的時間是個虛數,所以無法用圖或模型來表示。這裡又冒出來一個叫做虛數的討厭的數學概念,使用數學武器求解物理問題時,難免會陷入這樣的窘境。不管怎樣,按霍金的辦法去做的話,就會出現‘過去存在過虛時間’這樣的事情,如果我們把過去看成虛時間的話,就可以不帶奇點地‘平坦地’解釋宇宙的初始與終結。筆者絕對沒有抬出虛數為難大家的意思,不過,在繼續我們的話題之前有必要介紹一下虛數的概念以及它‘在實際問題中所代表的含義’。
虛時間引發大爆炸
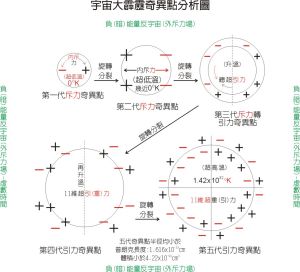
宇宙的創生是我們用虛時間研究的問題之一。最初,能量被封閉在非常非常狹小的空間裡,四周是無法逾越的高牆,但是根據量子力學的隧道效應,裡面的能量會貫穿牆壁跑到外面……這是量子宇宙論對大爆炸起因的解釋。筆者在這裡想說的是,利用虛時間也可以解釋大爆炸的發生。
假設在宇宙的最初(如同霍金所提倡的)時間是虛數,由於加速度為距離除以時間的平方,所以當時間為虛數時,力的符號變為負(反方向)。難以逾越的高牆反過來變成了深深的塹壕,在力學上勢能(位置能)的符號發生了變化,封閉著能量的口袋在一瞬間消失,從而揭開了宇宙大爆炸的序幕,在此瞬間裡時間由虛變實,變成了通常的膨脹。
利用虛時間不僅能消除奇點,而且還能解釋大爆炸的起因。話題似乎又轉回到了一開始的問題上:虛時間是什麼?由虛變實是怎么一回事?那個過程給周圍帶來了哪些變化?……這些事情都超越了我們的想像。
解釋
例如,在氫原子裡有一個電子,按照玻爾的舊量子論,電子是繞原子核公轉的粒子,即,電子是個顆粒,它圍繞著原子核鏇轉。經典力學的模型不難理解。
但是創立於本世紀20年代的新量子力學指出,應該把電子理解成是聚集於原子核周圍的雲團,電子不是一個顆粒,而是一團雲。為了用數學公式描述這團雲,就得使用複數,電子以及其它的微觀對象都屬於複數範疇,金屬中的自由電子以及封閉箱子裡的氣體分子的狀態原則上都要用複數來記述。因此,虛數已經大量地介入到了物理學之中。虛數不是個不明不白的數嗎?用它記述的對象是什麼東西呢?量子力學認為粒子具有波的性質,數學上用波函式描述波的狀態,然而波函式是個複數。
所謂複數波是什麼樣的波呢?無人能夠畫出它的圖象。波函式描述的是對象物(原子或電子)的狀態,而不是眼睛所看見的影象。人眼所能看到的是螢屏上出現的波紋狀的痕跡——它對應於物體的能量的大小及變化。
波函式的確表示了粒子的存在位置,不過我們計算空間中粒子的存在機率時必須把複數平方(正確的說法是,複變函數與它的共軛函式相乘)後轉變成實數才行。計算某個波函式所表示的粒子的能量時,我們通過求解量子力學的公式得出的是實數的能量值(在量子力學中稱為本徵值)。
這段文字或許令您費解,讓我們再複述一遍其中的要點。用於描述粒子狀態的波函式是由實數與虛數的和構成的複數,通過對式子進行變換一定能得出實數值,這種方法就是量子力學,我們把用量子力學公式求出的所謂各物理量的理論值與實驗測量值相對比進行各種分析,雖然人無法看見複數所表示的東西,但是這樣做並不矛盾。
量子力學真是妙不可言,測量數值是實數,而誰也看不到的狀態卻用奇妙的複數來表述。
那么,是不是可以認為複數所表述的狀態是真實的存在呢?
例如,某個電子的狀態用複數來記述,求解它的能量時,使用量子力學公式來計算得出了實數值,沒有問題。結果沒有問題能否說明其餘一切也都沒有問題呢?愛窮根究理的人(或形而上地研究問題的人)一定會拘泥於這樣的困惑。
電子在被觀測到之前,它的能量大小及存在位置均為不明,雲一樣存在的電子真的是個複數的東西呢?還是,因為我們對觀測之前的事情一無所知,為了方便起見才使用了數學家創造的複數呢?電子的實體就是虛數呢?還是,虛數根本沒有實體,使用虛數隻不過是為了能夠順利地進行以後的各種計算呢?
一場哲學爭論好象開始了,關鍵的是,無論持哪一種觀點都不會給以後的研究帶來妨礙。物理學家們好象並不願意過分深入地探討這些純哲學的問題。如果一定要說清楚的話,以玻爾為首的哥本哈根學派似乎持有粒子本身就是複數的觀點,與此對立,對作為量子力學基礎的‘不確定性’持反對意見的愛因斯坦等人則認為宇宙的根本是實數的東西,他們的真實思想,筆者無從知曉。總之,如果有一百位物理學家的話,大概就會有一百種對量子力學的解釋……
四維的勾股定理
 虛時間
虛時間反正示意圖是畫不出來的,普通的時間尚無法看見,更別提看見虛時間了。我們的意識在一定程度上能夠推定時間的經過,如果這時間是虛時間的話將會怎樣呢?誰也說不出來。霍金為了避開奇點用數學公式表示了時間的連續性,但是他卻迴避不了大爆炸前的虛時間。
虛時間的提出,消除了宇宙創生於奇點的困惑。接下來,筆者用比較易懂的狹義相對論的公式,再對虛時間進行一些講解。
狹義相對論認為,光速是不變的,長度及時間隨測量方法的不同而不同,時間與長度具有同等的資格。因此狹義相對論的公式是四維公式。
設x、y、z為三維空間坐標的互相垂直的三個軸,t為時間。為了使時間成為用長度表示的維,把時間與光速c的乘積ct作為代表第四維的軸。
假定光從A點出發沿直線(按狹義相對論觀點)到達B點,所需時間為t,則AB間的直線距離為ct。一般地說,時間軸與x、y、z軸中的任何一個軸都不是互相垂直的,長度ct中含有各個軸的成份,光走過的距離ct相當於以x、y、z為三邊的立方體的對角線之長,滿足三維勾股定理
(ct)2 =x2 +y2 +z2 。
也可以寫成
-(ct)2 +x2 +y2 +z2 =0。
如果將相對論的時間記述為三維空間裡的一維時間的話,-(ct)2 與x2 、y2 、z2 之和總應該為零。請注意:在數學處理上必須不帶任何區別地看待時間與空間。四維幾何學很難用我們的常識去理解,在四維幾何學裡從一開始就把ct作為一個獨立的坐標,而不是光傳播於x、y、z三維空間裡……。四維空間中的距離並不一定為零,而是一個定數,四個維的平方之和表示四維超立方體對角線的平方(稱為擴張的勾股定理),即,在四維幾何學中,時間與空間之間存在下述關係:
-(ct)2 +x2 +y2 +z2 =(常數)=S2
S是個定值,與光從A到B的過程有關。
這個公式是四維時空間裡的物理學公式。在原來的勾股定理中,各邊的平方均為正值,只有與時空間有關的時間項的平方為負值,也就是把-(ct)2 看作是加上一個負的項。
奇點的消除
 虛時間
虛時間但是,把這個規律套用到北極點上就會遇到困難,因為從北極點引出的線都是經度線,如圖所示在那裡距離的平方只有負數值,所以必須特殊地對待北極點——不得不把它看作奇點。這個模型叫做弗里德曼宇宙的時空。
為了迴避奇點,霍金等人使用了德西特的時空模型。在弗里德曼模型里,北極點象尖屋頂一般地突起,而德西特模型則圓滑地象個皮球,北極點與其它點一樣,看上去沒有任何不同。
在北極點附近,即宇宙的初期(或宇宙還很微小的時期——因為在霍金的理論中並沒有規定宇宙的起點)時間為虛數it,於是時間項的平方
-(ict)2=(ct)2就成了正值,因而在北極點及其附近的任何位置,時間及空間的平方都是正值,沒有任何特別的點。
時間是虛的嗎
剛才介紹了利用虛時間消除奇點的方法。此時此刻各位讀者大概是一種似懂非懂的心情,對數學式子按部就班地進行拆解是難度很高的工作,況且時間到底是什麼?當你意識到這個問題的同時,也會感到它的難度。讓我們到下一章再繼續探討有關時間的問題。前文中出現了由狹義相對論導出的公式
ct)2 +x2 +y2 +z2 =S2 ,
這個公式是否在暗示我們時間是個虛數呢?聰明的讀者一定意識到了這一點。勾股定理中的各平方項都應該是正的……。
上一節講過,這個公式是擴展了的勾股定理,該命名本身就不同於各平方項均為正值的普通的勾股定理,擴展的勾股定理表示了四維時空中的光速不變性。如果想把它改成勾股定理的原樣的話,就必須把時間定義為虛數it。
在除了量子力學以外的場合,我們所碰到的物理量都是實數,然而在這裡當我們按正統的勾股定理的觀點求平方根的話,時間卻成了虛數。
於是,有的哲學家(?)認為,現實的時間本身就是虛數,這種觀點的確有它的道理。從過去到將來推動包括我們自己在內的整個世界的‘時間’是實實在在的呢?還是虛無漂渺的呢?與長度及質量不同,時間在某種意義上說是無法感受的,它或許是虛的。不過……無論用什麼樣的辭彙去表達,坦率地說,誰也說不清楚。
如果從x2 +y2 +z2 =(ct)2 出發換一種寫法,把空間坐標移到等號右邊的話,擴展後的勾股定理就變成
(ct)2 -x2 -y2 -z2 =r2 ,
r為四維時空間裡的某個定值。這時,時間成了‘確確實實’的量,而空間(x、y、z)卻成了虛量……,在數學上,這樣做沒有什麼不可以的,但是從物理學的角度來看,這樣做畢竟離現實世界太遠,沒有說服力。只從純哲學的意義(?)去討論讓哪一項為負的問題,大概不會有任何價值吧。