無窮小量
定義
 等價無窮小量
等價無窮小量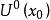 等價無窮小量
等價無窮小量設 在某 上有定義。若
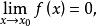 等價無窮小量
等價無窮小量 等價無窮小量
等價無窮小量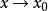 等價無窮小量
等價無窮小量則稱 為當 時的無窮小量。
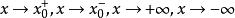 等價無窮小量
等價無窮小量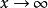 等價無窮小量
等價無窮小量類似地可以定義當 以及 時的無窮小量。
性質
(1)兩個(相同類型的)無窮小量之和、差、積仍為無窮小量。
(2)無窮小量與有界量的乘積為無窮小量。
等價無窮小量
定義
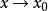 等價無窮小量
等價無窮小量 等價無窮小量
等價無窮小量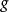 等價無窮小量
等價無窮小量設當 時, 與 均為無窮小量。若
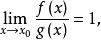 等價無窮小量
等價無窮小量 等價無窮小量
等價無窮小量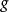 等價無窮小量
等價無窮小量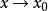 等價無窮小量
等價無窮小量則稱 與 是當 時的等價無窮小量 。記作
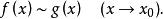 等價無窮小量
等價無窮小量性質
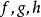 等價無窮小量
等價無窮小量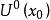 等價無窮小量
等價無窮小量設函式 在 上有定義,且有
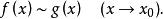 等價無窮小量
等價無窮小量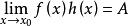 等價無窮小量
等價無窮小量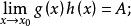 等價無窮小量
等價無窮小量(1)若 ,則
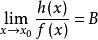 等價無窮小量
等價無窮小量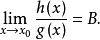 等價無窮小量
等價無窮小量(2)若 ,則
常用的等價無窮小量
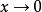 等價無窮小量
等價無窮小量(1)當 時,常用的等價無窮小量
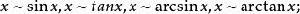 等價無窮小量
等價無窮小量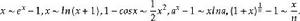 等價無窮小量
等價無窮小量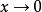 等價無窮小量
等價無窮小量(2)當 時,由基本等價無窮小量派生常用等價無窮小量
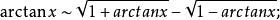 等價無窮小量
等價無窮小量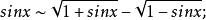 等價無窮小量
等價無窮小量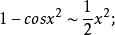 等價無窮小量
等價無窮小量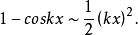 等價無窮小量
等價無窮小量套用
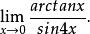 等價無窮小量
等價無窮小量(1)求極限
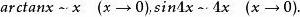 等價無窮小量
等價無窮小量解:由 所以
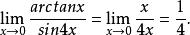 等價無窮小量
等價無窮小量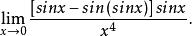 等價無窮小量
等價無窮小量(2)求極限
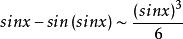 等價無窮小量
等價無窮小量解:由 可得
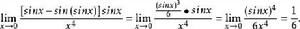 等價無窮小量
等價無窮小量