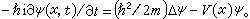泛函積分
正文
無限維分析學的一個新分支。它起源於量子物理學中的連續積分和機率論中的隨機過程的樣本空間的研究。目前，泛函積分方法已深入到分理化量子場論、基本粒子理論、隨機力學、馬爾可夫場、統計物理和湍流理論等領域。同時，泛函積分正在與群表示論、巴拿赫空間幾何學、微分方程論、隨機過程理論相互滲透。這一切都使它成為現代分析學中的一個令人矚目的學科。泛函積分的內容目前主要包括連續積分、柱測度、正定函式、擬不變測度理論等。連續積分 連續積分是指泛函沿著一類連續軌道的積分。1942年R.P.費因曼從最小作用量原理出發定義路徑積分,它給出量子力學的另一種等價的表達形式,後人稱為費因曼路徑積分，目前它已在量子物理中被愈來愈多地引用。為簡單起見，以有限個自由度的量子力學體系為例。通常這種體系的狀態用滿足薛丁格方程的復值的波函式Ψ描寫。例如,質量為m 的粒子在勢能場V(x)中的運動，這時Ψ滿足方程
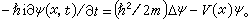
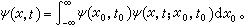量子力學的一個基本問題是求出Ψ (x,t)或Ψ(x,t；x0,t0)的表達式。 按照經典力學的觀點,質量為m的粒子在勢能場V(x)中運動的拉格朗日函式為
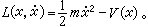設 x(τ)是一條連續路徑，適合條件x(τ0)=x0，x(τ)=x,那么沿著路徑的作用量為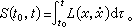 
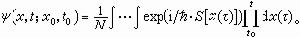
從數學的角度看，路徑積分是沒有經過嚴格定義的概念，最通常的理解是，先將【t0,t】進行n等分,記
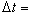
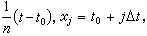0≤j ≤n。作依次連線（xj,jΔt）的折線xn(τ),設
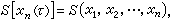作n重積分 
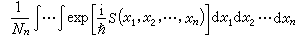
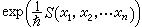是隨著n的增大而劇烈振盪的函式,故上述的極限實際上是不存在的。但費因曼積分非常富有啟發性，許多物理學家運用這種路徑積分及按他們的物理構想所提出的一些計算法則能很好地說明量子物理中的許多問題，例如從量子力學到經典力學的過渡等。同時，在量子場論中也出現了大量的類似的沒有嚴格定義的連續積分。這就向數學家提出了建立路徑積分的嚴格的數學基礎的要求。它是泛函積分研究的重要課題之一。近40年中，人們利用解析開拓、廣義函式、復值測度和振盪積分等各種手段去進行研究，但至今尚未解決。 泛函積分與微分方程 早在路徑積分出現以前，N.維納在研究作布朗運動的粒子的統計規律時已提出維納測度。設t>0，C表示【0,t】區間上連續並在0點取值為零的函式全體（C 中的每個元素可理解為作一維布朗運動的粒子的軌道）。又設(αi,bi)，1≤i≤n，是n個區間，
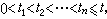稱集合A＝{x|x∈C,x(ti)∈(αi，bi),1≤i≤n}是C中的柱集。那么，軌道x 落入A中的機率是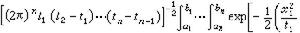 
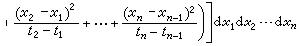
M.卡茨研究了一類泛函在作布朗運動的粒子所有軌道上的平均值的計算。設F是C上的連續泛函，這個平均值就是F關於維納測度的數學期望
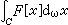。對連續軌道x作依次連線
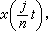1≤j≤n的折線xn(t),記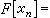
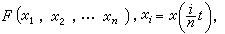1≤i≤n，則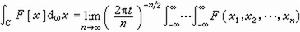
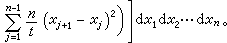引用費因曼的記號,上式可改寫為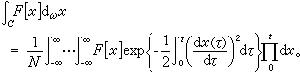 
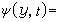
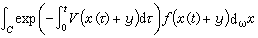在一定條件下滿足方程
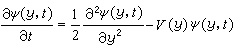，Ψ(y,0)=ƒ(y)。 這項工作開闢了用泛函積分研究微分方程的新方向，至今也還是泛函積分中的一個十分有意義的研究領域。
柱測度 柱測度是測度概念的推廣，它也是研究具有無限多個參數的隨機過程(廣義隨機過程)的重要工具之一。設φ是拓撲線性空間,(Ω,P)是機率空間，如果給定一族依賴於φ中的元素φ 的隨機變數{X(·,φ),φ∈φ }，滿足線性關係
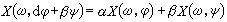（等式關於P幾乎處處成立）;則稱它是φ上的線性過程。另外,如果對φ中任何一個收斂於0的定向序列{φλ,λ∈Λ}，隨機變數序列{x(·,φλ)，λ∈Λ}依機率收斂於0,則稱{x(·，φ),φ∈φ }為廣義 (線性)隨機過程。根據柯爾莫哥洛夫機率測度存在性定理，在φ的代數對偶空間φA（φ上的線性泛函全體）上存在σ 代數B和機率測度μ，使得φA上的由φ
(ƒ)=ƒ(φ)(φ∈φ，ƒ∈φA)定義的函式φ關於B可測，而且若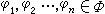
，則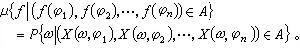 
這裡的基本問題之一是研究μ 能否集中在一個比φA更小的線性子空間W上，以便對廣義隨機過程{x(·，φ)，φ∈φ}的樣本軌道X(ω，·)作比較深入的研究。尋找樣本空間W 的問題等價於研究柱測度的可列可加性。
設X,Y是兩個實的線性空間，〈x,y〉,x∈X，y∈Y是X×Y上的實的雙線性泛函,並且對X中的任何非零向量x，必定存在y∈Y，使〈x,y〉≠0，對Y空間也有同樣假定。在X中任取n個向量x1,x2,…xn，記Y 中使<x1,·>,<x2,·>,…,<xn,·>可測的最小σ代數為F(x1,x2,…,xn)。F(x1,x2,…,xn)中的集稱為Y中的柱集，柱集全體記為φ，它是Y上的代數。設μ是φ上的集函式,μ 限制在每一個F(x1,x2,…,xn)上是一個機率測度，稱為Y上的柱測度。當X是拓撲線性空間時，如果對任何ε>0，存在X中零的鄰域V，對任何x∈V，成立μ｛y||<x,y>|>1｝<ε，則稱μ 關於X 的拓撲是連續的。特別當{X (·，φ),φ∈φ }是廣義隨機過程時，取φA中的線性子空間W0，使得φ=0與對一切ƒ∈W0,ƒ(φ)=0等價。設X=φ，Y=W0,<φ，ƒ>=ƒ(φ)，定義
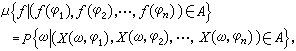
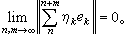令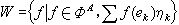
依機率收斂｝,則W上關於B的拓撲連續的柱測度是可列可加的。這個結果的重要性不但在於它是明洛斯定理的推廣而且在於它指出了柱測度可列可加性與巴拿赫空間結構的本質聯繫。 L.施瓦爾茨研究了將柱測度變換成可列可加測度的線性映射-拉東映射，提出了巴拿赫空間型的概念,在此基礎上建立了研究柱測度可列可加性的一般原理即施瓦爾茨對偶性定理。
正定函式表示 將是限維空間上深刻的調和分析理論推廣到無限維空間(拓撲線性空間或更一般的拓撲群)是無限維分析的主要課題。正定函式的表示問題就是其中之一。設G是拓撲群，e是G的單位元,ƒ(G)是G上的函式,ƒ(e)=1。如果對g中任意n個元素g1,g2,…gn和任意n個複數z1,z2,…zn，成立
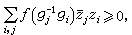，稱ƒ是g上的正定函式。 正定函式的表示問題和柱測度的可列可加性的關係極為密切。設φ 是拓撲線性空間，φ 按向量的加法成為交換的拓撲群。若ƒ是φ上的正定函式,W是φA上的線性子空間,且φ∈φ,φ=0等價於ƒ（φ）=0，對任何ƒ∈W；那么在W上有惟一的柱測度Λ，使
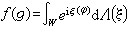(g∈φ)。ƒ是 φ上的連續的正定函式的充要條件是柱測度Λ關於φ 的拓撲是連續的。因此，經典調和分析中的有限維空間上的博赫納定理在無限維空間上的推廣問題與研究柱測度的可列可加性是等價的。當 G是一般的交換的拓撲群時，可用G的特徵標群GA代替φA進行類似的討論。根據關於柱測度可列可加性的明洛斯定理知道,核空間φ上的連續正定函式必是φ ┡上的機率測度的傅立葉變換。夏道行利用擬不變測度的理論對交換拓撲群上的正定函式的表示得到了很一般的結果，即對一類交換的拓撲群推廣了博赫納定理。 擬不變測度 設X是拓撲空間，B是X中開集全體張成的σ 代數。如果 g 是 X 上的雙射，並且對任何 A∈
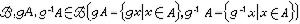，則稱g是(X，B)上可測同構。令G是(X,B)上可測同構全體所成的變換群。設μ是B上正則測度（即μ是滿足下列條件的測度：對任何 A∈B以及ε>0，必存在開集O，閉緊集F,使得O叾A叾F，並且μ(O-F)<ε）對任何G∈G，定義
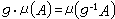，A∈B。如果對一切g∈g ，g·μ與μ都等價，則稱μ關於群g是擬不變的測度。 和連續積分一樣，擬不變測度的研究來源於量子物理。例如，量子場論中交換關係的表示問題實質上是和尋找某個拓撲線性空間上擬不變的機率測度問題等價的。又如相應於量子場論中真空態的測度就具有某個擬不變性質。這個事實推動了一般的擬不變測度理論的研究。夏道行利用測度論和運算元代數的方法率先對它們作了系統的研究，建立了一整套理論，獲得擬不變測度的許多基本性質，例如，證明了如下結果：設X是拓撲群，G是X的子群，G上有拓撲τ使(g,τ)成為第二綱的拓撲群，且G到X中的嵌入是連續的。對每個g∈G，定義左乘變換τg，如果(X,B)上存在有限的正則測度μ,它關於{τg,g∈G }是擬不變的，那么對B中每一個正測度的緊子集K,必然存在(G,τ)中單位元的鄰域V,當h∈V時，μ(K ∩τhK)>0。由此,立即可推出在無限維的巴拿赫空間E上不存在關於全空間平移擬不變的正則的機率測度。
另外,設P(x)是(X,B)上的非負可測函式,當g∈G時，定義p
(g)=本性下界(p(x)+p(τg_1x))(本性下界指在X中除去任意一個μ零集後在其上取下界,然後取這些下界的最大值）。 夏道行證明了下面的重要不等式：當(G，τ)又滿足第一可列公理時，對B中任一正測度集A，必有(G,τ)中單位元的鄰域V和正數с,使得對X上的任一非負可測函式p，成立
。
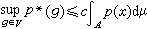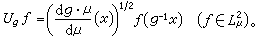
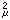上的對稱的弱閉運算元代數，夏道行利用對稱的弱閉運算元代數的分解定理，研究了擬不變測度的分解，證明對偶空間的存在，在這個基礎上建立了關於擬不變測度的L2傅立葉變換理論和相應的計算公式。看來，這個理論將為無限維空間上的微分方程、變分方程的研究提供工具。