定義
當變數值的項數N為奇數時,處於中間位置的變數值即為中位數;當N為偶數時,中位數則為處於中間位置的2個變數值的平均數。(注意:中位數和眾數不同,眾數指最多的數,眾數有時不止一個,而中位數只能有一個。)
| 按定額完成%分 | 工人數(人) | 向上累計次數 | 向下累計次數 |
| 80~90 90~100 100~110 110~120 120~130 130~140 140~150 | 5 11 14 27 20 14 9 | 5 16 30 57 77 91 100 | 100 95 84 70 43 23 9 |
| 合計 | 100 | —— | —— |
特點
1、中位數是以它在所有標誌值中所處的位置確定的全體單位標誌值的代表值,不受分布數列的極大或極小值影響,從而在一定程度上提高了中位數對分布數列的代表性。
2、有些離散型變數的單項式數列,當次數分布偏態時,中位數的代表性會受到影響。
3、趨於一串數的中間位置
計算
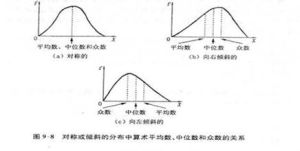 中位數
中位數設連續隨機變數X的分布函式為F(X),那么滿足條P(X≤m)=F(m)=1/2的數稱為X或分布F的中位數。
對於一組有限個數的數據來說,它們的中位數是這樣的一種數:這群數據里的一半的數據比它大,而另外一半數據比它小。計算有限個數的數據的中位數的方法是:把所有的同類數據按照大小的順序排列。如果數據的個數是奇數,則中間那個數據就是這群數據的中位數;如果數據的個數是偶數,則中間那2個數據的算術平均值就是這群數據的中位數。
中位數:也就是選取中間的數。一種衡量集中趨勢的方法。
要找中位數,首先需要從小到大排序,例如這組數據:23、29、20、32、23、21、33、25;
我們將數據排序20、21、23、23、25、29、32、33;排序後發現有8個數怎么辦?
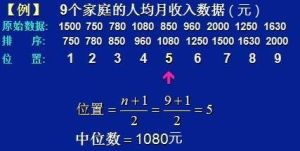
若有n個數,n為奇數,則選擇第(n+1)/2個為中位數,若n為偶數,則中位數是(n/2以及n/2+1)的平均數。
此例中選擇24為中位數
實例
 中位數
中位數第2組數:1、2、3、5的中位數是2.5。原理:如果總數個數是偶數的話,按從小到大的順序,取中間那兩個數的平均數.(2+3)÷2=2.5 第3組數:1、100、101、10000的中位數是100.5注意:中位數和數值的大小沒有絕對的關係。

