大樣本統計
正文
研究樣本大小n趨於無限時,統計量和相應的統計方法的極限性質(又稱漸近性質)，並據以構造具有特定極限性質的統計方法。例如,用樣本均值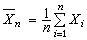
估計總體均值θ，在n→
時，
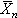以機率1收斂於θ(見機率論中的收斂),稱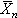為θ的強相合估計。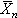的這個性質只有在n→時才有意義，這叫做大樣本性質,而強相合性的研究屬於大樣本統計的範圍。根據統計量的極限性質而得出的統計方法稱為大樣本方法。例如:設X1,X2,…,Xn是從正態總體N(μ,σ2)中抽出的樣本，μ和σ未知，要作μ的區間估計。記樣本方差為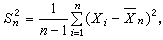 
當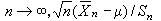 
依分布收斂於標準常態分配N（0,1）。基於這個性質可知, 當n較大時,可用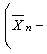
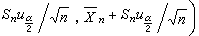作為 μ 的區間估計，其中
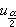是標準常態分配的上
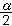分位數（見機率分布）；這個估計的置信係數當n→時趨於指定的 1-α(0<α<1)。這就是一個大樣本方法。 與大樣本性質和大樣本方法相對，小樣本性質是指在樣本大小n固定時統計方法的性質,小樣本方法是指基於n固定時的統計量性質的統計方法。如上述第一例,當n固定時有E
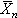=θ,即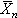為θ的無偏估計(見點估計);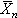的這個性質在n固定時有意義,所以是小樣本性質。又如，英國統計學家W.S.戈塞特(又譯哥色特，筆名“學生”)在1908年找到了
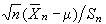的精確分布為自由度是n-1的t分布(見統計量)。基於此事實,可知對任何固定的n,μ的區間估計
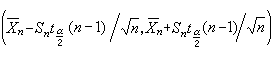具有確切的置信係數1-α。其中
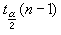是自由度為n-1的 t分布上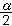分位數。這個性質對任何固定的 n都成立。因而上述區間估計是小樣本方法。總之，區分大、小樣本性質（或方法）的關鍵在於樣本大小 n是趨於無限還是固定，而不在於n數值的大小。 小樣本方法也稱為“精確方法”，因為它往往是基於有關統計量的精確分布（如前例中的t分布）;與此相應，小樣本方法的統計特性，如顯著性水平（見假設檢驗）、置信係數(見區間估計)等，往往是精確而非近似的。與此相對，大樣本方法也稱為“漸近方法”或“近似方法”，因為它是基於統計量的漸近分布，且有關的統計特性只是近似而非精確的。在套用中,樣本大小n總是一個有限數，這裡就有一個近似程度如何的問題。如在對N（μ,σ2）中的μ作區間估計的例子中，指定的置信係數為0.95，按大樣本理論作出區間估計
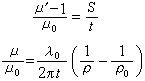
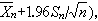當n→時,其置信係數趨於0.95,但即使n很大,置信係數也只是接近而非確切等於0.95。為了在使用它時做到心中有數，需要在n固定的情況下,對真實的置信係數與其近似值0.95的差距作出有用的估計，在大樣本方法的使用中，一般都存在此問題。但由於數學上的困難，目前使用的許多大樣本方法中，通常很少有有效的誤差估計，這是大樣本方法的弱點。然而它仍有重要的理論和實際意義：它不僅提供了一批可供選用的統計方法，而且，經驗證明，當一個統計方法不具備某些基本的大樣本性質（如相合性）時，常常也很難有良好的小樣本性質。評價一個統計方法的優良性時，大樣本性質是不可忽視的。 相合性，是一項重要的大樣本性質。一般地說，統計方法的相合性是指：只要樣本大小n足夠大,則使用這個統計方法時，可以用任意確切的程度回答所提出的統計推斷問題。例如,估計的相合性是表示,當n→
時,估計量在一定意義下，如依機率收斂或幾乎必然收斂或以r階平均收斂 (見機率論中的收斂)於被估計值。檢驗的相合性是指它在任意指定的備擇假設處的功效當 n→時趨於 1。相合性是最基本也是最容易滿足的大樣本性質。還有漸近無偏性、漸近有效性（見點估計）、和漸近正態性，或更一般地，漸近於某種特殊的極限分布的性質，也都是重要的大樣本性質。 大樣本統計的發展，依賴於機率論的極限理論，它在一定程度上已構成機率論極限理論的一個方面。1900年K.皮爾森證明了關於擬合優度的ⅹ2統計量的分布漸近於ⅹ2分布的著名定理，可以作為大樣本理論的發端。更早一些，在機率論中就證明了關於二項分布漸近於常態分配的定理，這個定理也可用於大樣本統計方法（求二項分布參數的大樣本區間估計），但習慣上把這定理看作是純粹機率論的定理。自1900年以後，特別是二次大戰後的30多年中，大樣本理論發展很快，達到了相當深入的地步，重要的結果有：關於擬合優度的ⅹ2檢驗漸近於ⅹ2分布的理論，最大似然估計及一般漸近有效估計的理論，似然比檢驗及一般漸近有效估計的理論，穩健估計大樣本理論以及非參數統計中大量的大樣本理論。現在，大樣本理論在數理統計學中仍是一個活躍的研究方面。（見假設檢驗、點估計、穩健統計）
參考書目
J. Serfling,ApproxiMation Theorems in MatheMatical Statistics, John Wiley & Sons, New York,1980.
