簡介
創立者
小樣本理論和方法的創立者是威廉.西利.戈塞特(William Sealy Gosset,1876-1937),他是英國統計學家,是現代統計方法及其套用於實驗設計與分析的先驅。
形成背景
小樣本理論的系統形成,是19世紀初葉的事情。小樣本分布在統計假設檢驗和區間估計等方面的套用,可以省人、省錢、省時間,因而,引起了工業、農業和科學研究等實際工作者的重視和歡迎;同時,也吸引更多的統計學家開拓這方面新的領域,這樣便推動著小樣本理論及其套用不斷地向縱深發展。
容量標準
當樣本容量 n<50 的時侯,構造統計量一般不能藉助於大樣本理論。這時,統計量的分布為與常態分配不同的新分布,於是產生小樣本分布的理論。
常見分布
 小樣本理論
小樣本理論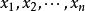 小樣本理論
小樣本理論 小樣本理論
小樣本理論 小樣本理論
小樣本理論在小樣本理論里,最常見的分布有:t 分布, 分布和 F 分布。一般說來,從正態總體裡,隨機抽取容量為(n<50)的樣本 ,構造 變數, 變數和 F 變數等統計量,研究這些統計量的機率分布和性質等,形成了小樣本統計方法的系統理論。
定義
小樣本理論是樣本理論的一個分支,樣本分布與樣本的數量 n 有關,小樣本理論是討論樣本數 n 較小的樣本分布問題。
小樣本理論(small sample theory)亦稱精確樣本理論,統計量性質的一種刻畫,它研究樣本容量固定時,各種統計量的性質及由此進行的統計推斷。精確樣本理論最早的例子是由英國統計學家和化學家戈塞特(Gossett , W. S.)於1908年提出的 t 分布。
理論系統
卡方分布
 小樣本理論
小樣本理論 小樣本理論
小樣本理論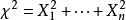 小樣本理論
小樣本理論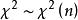 小樣本理論
小樣本理論設 獨立同分布於標準常態分配 ,則 的分布稱為自由度為 n 的卡方分布,記作 。
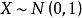 小樣本理論
小樣本理論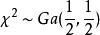 小樣本理論
小樣本理論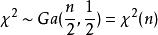 小樣本理論
小樣本理論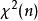 小樣本理論
小樣本理論若隨機變數 ,則 ,根據伽馬分布的可加性有 ,由此可見 分布是伽馬分布的特例。
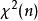 小樣本理論
小樣本理論(1) 分布的密度函式的圖像是一個只取非負值的偏態分布,其具體表達式為:
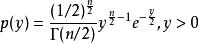 小樣本理論
小樣本理論(2)它的期望等於自由度,方差等於2倍自由度,即:
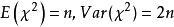 小樣本理論
小樣本理論F分布
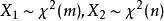 小樣本理論
小樣本理論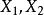 小樣本理論
小樣本理論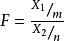 小樣本理論
小樣本理論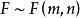 小樣本理論
小樣本理論設隨機變數 ,其中 獨立,則稱 的分布是自由度為 m 與 n 的 F 分布,記作 ,其中 m 稱為分子自由度,n 稱為分母自由度。
(1)F 分布的密度函式是一個只取非負值的偏態分布,表達式為:
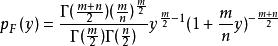 小樣本理論
小樣本理論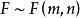 小樣本理論
小樣本理論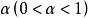 小樣本理論
小樣本理論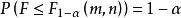 小樣本理論
小樣本理論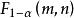 小樣本理論
小樣本理論 小樣本理論
小樣本理論(2)當隨機變數 時,對給定 ,稱滿足機率等式 的 是自由度為 m 與 n 的 F 分布 分位數;
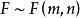 小樣本理論
小樣本理論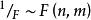 小樣本理論
小樣本理論(3)由 F 分布的構造可知,若 則有 。
t分布
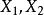 小樣本理論
小樣本理論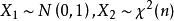 小樣本理論
小樣本理論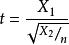 小樣本理論
小樣本理論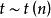 小樣本理論
小樣本理論設隨機變數 獨立,且 ,則稱 的分布為自由度為 n 的 t 分布,記為: 。
(1)t 分布的密度函式的圖像是一個關於縱軸對稱的分布,與標準常態分配的密度函式形狀類似,只是峰比標準常態分配低一些,尾部的機率比標準常態分配大一些;自由度為 n 的 t 分布密度函式的具體表達式為:
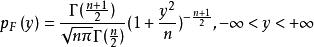 小樣本理論
小樣本理論(2)自由度為1的 t 分布就是標準柯西分布,它的均值不存在;
(3)n>1 時,t 分布的數學期望存在且為0;
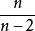 小樣本理論
小樣本理論(4)n>2 時,t 分布的方差存在,且為 ;
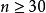 小樣本理論
小樣本理論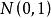 小樣本理論
小樣本理論(5) 當自由度較大(如 )時,t 分布可以用 分布近似。