背景和動機
在序理論的很多特定領域中，我們限制於帶有特定界限構造是完全的偏序集合類。例如在格理論中，人們感興趣於所有有限非空子集都有最小上界和最大下界的那些次序。在域理論中，人們關注所有有向子集都有上確界的那些偏序集合。完全格和帶有最小元素（“空上確界”）的次序提供了進一步的例子。
在所有這些情況中，極限扮演了理論的中心角色，它由各種學科的特殊套用中對它們的解釋所支持。不奇怪人們還感興趣於指定在這種次序間的適當映射。從泛代數的角度，這意味著人們希望為所考慮的結構找到適當的同態概念。通常通過考慮那些相容於作為各自次序的特徵的構造的函式來完成。例如，格同態是保持非空有限上確界和下確界的這種函式，就是說兩個元素的上確界/下確界的像就是它們的像的上確界/下確界。在域理論中，人們經常處理保持所有有向上確界的所謂的Scott連續性函式。
下面給出的定義和術語的背景可在範疇論中找到，其中考慮更一般意義的極限（和“上極限”）。 極限保持和 極限反射函子的範疇論概念完全協調於序理論，因為次序可以被認為是特定種類的小範疇。
形式定義
考慮兩個偏序集合 P和 Q，和從 P到 Q的函式 f。進一步的，設 S是有最小上界 s的 P的子集。則 f 保持 S的上確界，如果集合 f( S) = { f( x) | x∈ S}在 Q中有等於 f( s)的最小上界，即
f(supS) = supf(S).
注意這個定義由兩個要求組成：集合的上確界 f( S)存在並且它等於 f( s)。這對應於上面提及的範疇論相應者，但在文獻中不總是要求。事實上，在某些情況下人們弱化定義為只要求存在的上確界等於 f( s)。但是這裡採用上面給出的普通概念並在需要的時候明確的聲明其他要求。
從上面給出的基本定義，人們可以推導出廣泛的有用的性質。在偏序集合 P和 Q之間的函式 f被稱為保持有限、非空、有向或任意上確界，如果它分別保持所有有限、非空、有向或任意集合的上確界。非空有限上確界的保持還可以定義自恆等式 f( x∨ y) = f( x)∨ f( y)，對於所有元素 x和 y成立，這裡假定∨是在兩個次序上的全函式。
對偶的，可定義下確界保持的性質。
與極限保持的“相反”條件叫做反射。考慮如上函式 f和 P的子集 S，使得sup f( S)存在於 Q中並且等於對某個 P的元素 s的 f( s)。則 f 反射 S的上確界，如果sup S存在並且它等於 s。如同對保持所展示的那樣，可以通過考慮特定類的集合 S和通過對偶化下確界定義而獲得很多額外的性質。
特殊情況
從上述定義中導出的一個特殊情況或性質有其他名字或在序理論的某些領域中特別重要。例如，保持空上確界的函式是保持最小元素的函式。進一步的，由於在前面解說的動機，很多極限保持函式作為特定序結構的專用的同態。下面給出其他一些突出的例子。
保持所有極限
如果函式 保持所有上確界（或下確界）則出現一個有趣的情況。更精確地說，這被表達為聲稱一個函式保持所有“現存”上確界（或下確界），所考慮的偏序集合不是完全格也可以如此。例如，（單調）伽羅瓦連線有這個性質。反過來說，通過序理論的伴隨函子定理，保持所有上確界/下確界的映射只要滿足額外的條件就可以被當作伽羅瓦連線的一部分。
分配律
格 L是 分配格，如果對於所有 L中的 x, y和 z，滿足
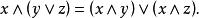極限保持函式但是這只是聲稱了 交函式∧： L-> L 保持二元上確界。在格理論中已知這個條件等價於它的對偶條件，就是說函式∨： L-> L保持二元下確界。以類似的方式，可見到完全Heyting代數的無窮分配律
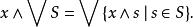極限保持函式（參見無點拓撲學）等價於交函式∧保持任意上確界。但是這個條件不適用於它的對偶。
Scott-連續性
保持有向上確界的函式叫做Scott連續性的或有時就叫“連續的”，如果不混淆於數學分析和拓撲學的對應概念的話。在範疇論也能找到對極限保持的術語連續。
重要性質和結果
上述極限保持的定義非常強壯。實際上，至少保持兩元素鏈即兩個可比較元素的集合的上確界或下確界的所有函式必然是單調的。因此，所有上述規定的特殊保持性質都引發單調性。
基於某些極限可以被以其他極限來表達的事實，人們可以推導在保持性質之間的聯繫。例如函式 f保持有向上上確界若且唯若它保持所有理想的上確界。進一步的，來自其中所有非空有限上確界存在的偏序集合（所謂的sup-半格）的映射 f保持任意上確界，若且唯若它保持有向和有限制（可能為空）上確界二者。
但是，保持所有上確界的函式也保持所有下確界或反之都不是真的。
