背景
極限學習機(Extreme Learning Machine, ELM)在2004年由Guang-Bin Huang、Qin-Yu Zhu和Chee-Kheong Siew提出,並發表於當年的IEEE國際互動會議(IEEE International Joint Conference)中,目的是為了解決反向傳播算法(backward probagation)學習效率低、參數設定繁瑣的問題 。2006年,ELM原作者在對算法進行了進一步的測評後,將結論發表至Neurocomputing並獲得關注 。
ELM最初是為監督學習問題而設計的,但在隨後的研究中,其套用範圍被推廣至幾乎所有機器學習領域,包括聚類 和特徵學習 (representational learning)等,並出現許多變體和改進算法。在ELM的發展過程中,南洋理工大學的Guang-Bin Huang等人作為ELM的原作者,對ELM的理論和套用進行了持續的研究 。ELM的學習策略被認為與某些生物學習過程相近 ,也為機器學習領域帶來了諸多啟發,影響了RKS (Random Kitchen Sinks)和No-Prop (No-Propagation)等算法。
結構
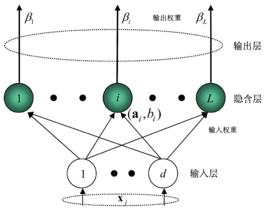
ELM在文獻中可以作為一種學習策略(類比於反向傳播算法),也可作為包含構築模組的神經網路進行論述。對於後者,ELM通常使用單層前饋神經網路(Single Layer Feedforward neuron Network, SLFN),但也可拓展至深度網路。具體地,SLFN的組成包括輸入層、隱含層和輸出層,其中隱含層的輸出函式具有如下定義 :
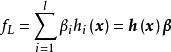 極限學習機
極限學習機 極限學習機
極限學習機 極限學習機
極限學習機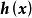 極限學習機
極限學習機這裡為神經網路的輸入、為輸出權重,被稱為特徵映射或激勵函式(activation function),其作用是將輸入層的數據由其原本的空間映射到ELM的特徵空間:
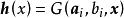 極限學習機
極限學習機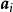 極限學習機
極限學習機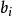 極限學習機
極限學習機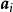 極限學習機
極限學習機式中和是特徵映射的參數,在ELM研究中也被稱為節點參數(node parameter),其中為輸入權重(input weights) 。由於ELM中輸入層至隱含層的特徵映射是隨機的或人為給定的且不進行調整,因此ELM的特徵映射是隨機的。依據通用近似定理,特徵映射可以是任意非線性的片段連續函式(piecewise continuous function),常見的有:
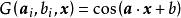 極限學習機
極限學習機三角函式:
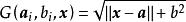 極限學習機
極限學習機高斯函式:
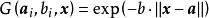 極限學習機
極限學習機徑向基函式:
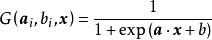 極限學習機
極限學習機Sigmoid函式:
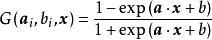 極限學習機
極限學習機雙曲正弦函式:
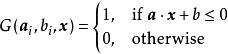 極限學習機
極限學習機硬限幅函式(hard limit function):
不同的隱含層節點可以有不同的映射函式,神經網路的節點也由其具有的特徵映射命名,例如Sigmoid節點、徑向基函式節點等。除上述被廣泛使用的映射函式外,SLFN的節點也可以是其它經過封裝的計算單元 ,例如模糊系統(fuzzy inference system)、其他次級神經網路等。
算法
標準算法
ELM僅需求解輸出權重,在本質上是一個線性參數模式(linear-in-the-parameter model),因此其學習過程易於在全局極小值收斂 。已知N組學習數據,對包含L個隱含層節點和M個輸出層節點的ELM進行學習有如下步驟 :
隨機分配節點參數:在計算開始時,SLFN的節點參數會隨機生成,即節點參數與輸入數據獨立。這裡的隨機生成可以服從任意的連續機率分布(continuous probability distribution)。
計算隱含層的輸出矩陣:隱含層輸出矩陣的大小為N行M列,即行數為輸入的訓練數據個數,列數為隱含層節點數。輸出矩陣本質上即是將N個輸入數據映射至L個節點所得的結果。
求解輸出權重:隱含層的輸出權重矩陣的大小為L行M列,即行數為隱含層節點數,列數為輸出層節點數。與其他算法不同,ELM算法中,輸出層可以沒有誤差節點,ELM算法的核心是求解輸出權重使得誤差函式最小。
1.隨機分配節點參數:在計算開始時,SLFN的節點參數會隨機生成,即節點參數與輸入數據獨立。這裡的隨機生成可以服從任意的連續機率分布(continuous probability distribution)。
2.計算隱含層的輸出矩陣:隱含層輸出矩陣的大小為N行M列,即行數為輸入的訓練數據個數,列數為隱含層節點數。輸出矩陣本質上即是將N個輸入數據映射至L個節點所得的結果。
3.求解輸出權重:隱含層的輸出權重矩陣的大小為L行M列,即行數為隱含層節點數,列數為輸出層節點數。與其他算法不同,ELM算法中,輸出層可以沒有誤差節點,ELM算法的核心是求解輸出權重使得誤差函式最小。
ELM使用的L1誤差函式(L1 loss function)有如下表示:
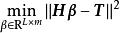 極限學習機
極限學習機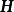 極限學習機
極限學習機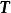 極限學習機
極限學習機 極限學習機
極限學習機這裡 為輸出矩陣, 為訓練目標, 為矩陣元素的弗羅貝尼烏斯範數(Frobenius norm)。引入L1正則化項後,上式改寫為:
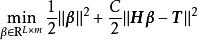 極限學習機
極限學習機 極限學習機
極限學習機其中為正則化係數(regularization coefficient)求解該誤差函式等價於嶺回歸問題,其解有如下表示:
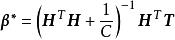 極限學習機
極限學習機此外奇異值分解(single value decomposition, SVD)也可用於求解權重係數:
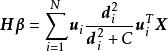 極限學習機
極限學習機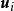 極限學習機
極限學習機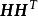 極限學習機
極限學習機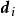 極限學習機
極限學習機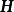 極限學習機
極限學習機式中 為 的特徵向量, 為 的特徵值。研究表明相對較小的權重係數能提升SLFN的穩定性和泛化能力 ,因此在複雜問題下ELM的正則化是必要的。
這裡以Python為例對ELM標準算法進行編程實現:
ELM算法中求解輸出權重的過程中有矩陣求逆的步驟。由於映射函式的初始化是隨機的,因此在實際計算中經常出現矩陣無法求逆的現象。在理論上只要設定較大的正則化參數,需要求逆的矩陣將始終是正定矩陣,但是過大的正則化係數會影響ELM的泛化能力。一個可行的改進方案,是在映射函式隨機初始化的過程中,僅選擇能使隱含層輸出矩陣達到行滿秩或列滿秩的參數。這一改進可見於徑向基函式 和Sigmoid函式 中,能夠使ELM算法在計算上更加穩定。
改進算法
ELM計算簡單,在複雜的機器學習問題中(例如MNIST ),與其它算法相結合也可以提供優良的表現。同時由於“不調整隱含層參數”是一個相對鬆散的定義,ELM的拓展和外延也非常豐富 。
動態算法
ELM中特徵映射的隨機初始化為其帶來了泛化的優勢,但也意味著相比於梯度下降算法,ELM的神經網路需要更多的節點。節點的增加帶來了計算量的增加,在訓練數據較多,尤其是大數據問題下,過多的節點會顯著消耗計算資源,並可能出現過度擬合。為解決上述問題,許多研究在原有ELM算法的基礎上提出了動態學習的解決方案,即在訓練過程中不斷改變隱含層節點數,並力求在學習效果最大和節點數最小間達到平衡。包含上述動態學習功能的改進版本包括增量式ELM(Incremental ELM, I-ELM)、雙向ELM(Bidirectional ELM, B-ELM)和自適應ELM(Adaptive ELM, A-ELM)等。
這裡以I-ELM為例說明。在開始階段,SLFN會被賦予一個可容忍的最簡結構,隨後整個學習過程以疊代方式進行,每一次疊代都會隨機產生數個備選節點,而對縮國小習誤差貢獻最大的一個節點會被選中並加入SLFN中進行下一次疊代,這樣當學習誤差疊代至預先設定的精度時,SLFN中不會有多餘的節點。
一些動態算法,例如I-ELM和自適應ELM能夠使用常見的激勵函式,而且被證明和標準算法一樣,保持了SLFN的通用近似定理 。
線上序列ELM
線上序列ELM (Online Sequential ELM,OS-ELM)是可以使用實時數據進行學習並更新輸出權重的ELM算法。OS-ELM的運行分為兩部分,首先,OS-ELM像ELM標準算法一樣通過給定的訓練數據計算輸出權重;隨後在線上學習的過程中,每當有新的數據塊被接收,就重新運行一次ELM並得到新的輸出權重,最後新舊輸出權重會進行組合從而完成對神經網路的更新,有些算法會在更新數據時加入遺忘函式 。這裡給出一個OS-ELM的簡單例子 :
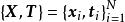 極限學習機
極限學習機輸入:學習數據;輸出:完成學習的ELM
 極限學習機
極限學習機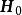 極限學習機
極限學習機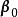 極限學習機
極限學習機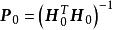 極限學習機
極限學習機初始化階段:定義;使用初始的學習數據和ELM標準算法計算輸出矩陣和輸出權重;定義
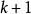 極限學習機
極限學習機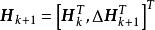 極限學習機
極限學習機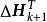 極限學習機
極限學習機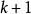 極限學習機
極限學習機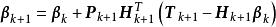 極限學習機
極限學習機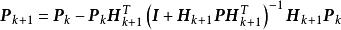 極限學習機
極限學習機線上學習階段:當第組學習數據可用時,計算新的輸出矩陣,其中為使用第組學習數據獨立計算所得的輸出矩陣。最後計算新的輸出權重,其中
偏斜與噪聲數據的改進算法
訓練數據的質量和標準化程度,對神經網路的運行有很大影響。偏斜數據難以被轉化至標準常態分配,會降低神經網路的學習效率;噪聲數據包含過多除學習目標以外的信息,會降低神經網路的泛化能力。加權ELM (Weighted ELM, W-ELM)是在分類問題中為應對偏斜數據對標準ELM進行改進的算法。加權ELM與標準算法的區別在於誤差函式的構建,標準算法中的正則化參數為一常數,而加權ELM將其修改為與輸入數據大小相同的矩陣,矩陣的元素被稱為懲罰係數(penalty coefficients)。懲罰係數能夠弱化偏斜數據中的多數成員對算法的影響。加權ELM的誤差函式可有如下表示:
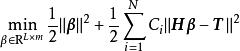 極限學習機
極限學習機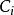 極限學習機
極限學習機式中即為懲罰係數。在加權ELM的基礎上,有研究提出了重加權ELM (re-weighted ELM),即以疊代方式加權的ELM算法。重加權ELM被證明具有更好的穩定性,能夠解決訓練數據中的異常值問題。
噪聲數據可理解為真實數據與擾動的疊加,對擾動在ELM算法中傳播的研究表明 ,使用特定的方式選取映射函式和輸入權重,能夠顯著降低輸入噪聲對輸出矩陣和輸出權重的影響。由此提出的FIR-ELM (Finite Impulse Response filte ELM)和DFT-ELM (Discrete Fourier Transform ELM)在初始化輸入層權重時使用了濾波技術,提高了算法對噪聲數據的穩定性。
其它變體
ELM模式集合
將機器學習方法進行模式集合的方法適用於ELM。常見的模式集合方法包括取平均、投票制(voting)、疊代(boosting)等,這裡以分類問題中的投票制的ELM模式集合進行說明 :
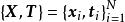 極限學習機
極限學習機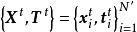 極限學習機
極限學習機 極限學習機
極限學習機輸入:學習數據、測試數據和個ELM;輸出:測試數據的學習結果
學習過程:使用學習數據對每個ELM進行獨立的訓練;測試過程:使用ELM對測試數據進行分類,匯總分類結果,輸出被分最多的類別。
非監督學習ELM
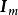 極限學習機
極限學習機ELM最初是為監督學習設計的,ELM的原作者在2014年以流型正則化(manifold regularization)技術為基礎提出了解決聚類和字元嵌入(embedding)問題的非監督ELM (unsupervised ELM, US-ELM)。具體而言,US-ELM的誤差函式中加入了流型正則化項():
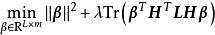 極限學習機
極限學習機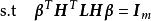 極限學習機
極限學習機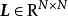 極限學習機
極限學習機其中是無標籤學習數據的拉普拉斯矩陣(graph Laplacian)上述最佳化問題被證明等價於一次廣義特徵值求解(Generalized Eigenvalue Problem, GEP):
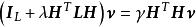 極限學習機
極限學習機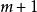 極限學習機
極限學習機輸出權重矩陣可以從第二組到第組特徵向量中獲得:
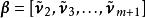 極限學習機
極限學習機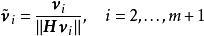 極限學習機
極限學習機對嵌入問題,US-ELM將直接輸出嵌入矩陣;對於聚類問題,US-ELM使用K-均值算法(k-means algorithm)對嵌入矩陣中的數據進行聚類。
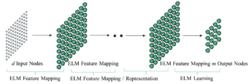 使用ELM作為自編碼器的多層ELM
使用ELM作為自編碼器的多層ELM深度結構的ELM算法
ELM以堆疊自編碼器(stacked autoencoders)的形式形成深度結構。在進行學習時,深度ELM前端的數個隱含層使用ELM訓練堆疊自編碼器對輸入變數進行特徵學習,並在最後一個隱含層中使用ELM對編碼後的輸入特徵進行學習。深度ELM在圖像處理等問題中的表現被證明優於ELM傳統算法,體現了深度結構的優勢。此外,ELM也可以僅進行特徵學習並將編碼的特徵輸出至其它算法。性質與理論
插值性質
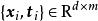 極限學習機
極限學習機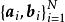 極限學習機
極限學習機在ELM的插值理論研究中有如下結論 :給定任意無限可導的激勵函式,對於N組訓練數據,存在隱含層節點數小於N的SLFN,在由ELM學習後,訓練誤差能逼近任意精度,且當SLFN隱含層節點數與訓練數據相同時,訓練誤差為零。這裡的激勵函式的參數可以由服從任意連續機率分布的隨機數在ELM學習中初始化。上述結論表明,從插值角度而言,只要隱含層節點數足夠,ELM能夠使得SLFN以任意精度擬合給定的訓練數據。
泛化性質
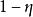 極限學習機
極限學習機ELM具有良好的泛化能力,其重要原因是算法中對特徵映射參數的隨機初始化增強了各輸入特徵的相互獨立性,創造了一個更大的求解空間,從而有利於SLFN找到正確的目標函式進行學習。對於回歸問題,研究表明,在使用多項式函式、Sigmoid函式和Nadaraya–Watson函式作為映射時,ELM較好地保持了SLFN原本的泛化能力 ;若使用高斯類函式作為映射,ELM的泛化能力將會降低,但使用正則化和模式集合技術能夠解決這一問題 。對於分類問題,ELM在統計學習角度被認為具有較小的VC維(Vapnik–Chervonenkis dimension),即ELM在泛化時擁有較小的實際風險(actual risk)上限。具體而言,對於包含L個無限可導特徵映射節點的ELM具有L個V-C維度 ,在泛化時,其機率下的實際風險為 :
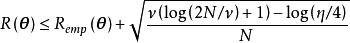 極限學習機
極限學習機 極限學習機
極限學習機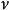 極限學習機
極限學習機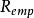 極限學習機
極限學習機式中為訓練數據樣本數,為V-C維度,為訓練數據所得的經驗風險(empirical risk)
通用近似定理
諸多研究證實了SLFN的通用近似定理(universal approximation theorem)適用性 ,而對ELM的研究表明,雖然ELM中SLFN的特徵映射是隨機的,但其依然服從該定理。ELM的通用近似定理有如下表述 :
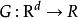 極限學習機
極限學習機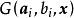 極限學習機
極限學習機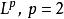 極限學習機
極限學習機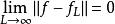 極限學習機
極限學習機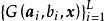 極限學習機
極限學習機對任意的非常數片段連續特徵映射如果在空間稠密,則,即SLFN可以無限趨近於任意連續的目標函式。這裡特徵映射序列可以由服從任意連續機率分布的隨機數在ELM學習中初始化。
ELM的通用近似定理適用於幾乎所有常用的激勵函式,且不要求激勵函式出處連續可導,閾值函式(threshold function)可以作為ELM的激勵函式。此外對於分類問題,ELM的通用近似定理可以有如下形式 :
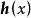 極限學習機
極限學習機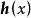 極限學習機
極限學習機 極限學習機
極限學習機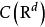 極限學習機
極限學習機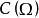 極限學習機
極限學習機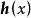 極限學習機
極限學習機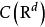 極限學習機
極限學習機 極限學習機
極限學習機對任意特徵映射,如果在維實數空間或其緊緻集上稠密,那么隱含層包含隨機初始化的泛化SLFN能夠區分在或上任意數量和形狀的不相交區域(disjoint region)。
在分類問題上的通用近似定理表述意味著,只要SLFN擁有足夠多的隱含層節點,ELM能夠無限趨近任意的決策邊界(decision boundary)。
生物學相似性
ELM被認為包含了生物學習的某些機制。例如在小鼠的實驗中,不同嗅覺信號從嗅小球(glomeruli)至嗅腦(piriform cortex)的映射被認為是分散和無差別的 ,即神經元對信號的加工與環境無關,這與ELM的輸入權重獨立於輸入數據和學習過程具有相似性。類似的學習機制在猴子的決策行為中也有出現 。在ELM原作者Guang-Bin Huang的論述中,ELM命名的含義即是超越和打破傳統機器學習與生物學習間的障礙。
(原文) ‘‘ ‘Extreme’ here means to move beyond conventional artificial learning techniques and to move toward brain alike learning. ELM aims to break the barriers between the conventional artificial learning techniques and biological learning mechanism.”
與其它算法的比較
研究表明,ELM在與反向傳播算法(Back-Propagation, BP)和支持向量機(Support Vector Machine, SVM)的比較中,其學習效率和泛化性能具有一定優勢 。
 ELM與BP和SVM回歸(SVR)算法的比較實例
ELM與BP和SVM回歸(SVR)算法的比較實例反向傳播算法
在與反向傳播算法的比較中,ELM的學習速度是前者的十倍以上,具有明顯的效率優勢。在效果方面,ELM與BP的學習精度相當,在基於回歸問題的諸多測試中,ELM有表現出更好的效果 ;同時也有研究表明,ELM在實際套用中的表現可能略低於BP算法 。
支持向量機
支持向量機是常被用於和ELM進行比較的算法,這裡列出一些兩者的不同:
ELM算法包含直接的特徵映射並且輸入層,隱含層和輸出層是連線的;SVM基於核方法(kernel method)的特徵映射是間接的,不考慮特徵在神經網路各層的連線。SVM在求解時構建了超平面(hyperplane)對數據點進行分類;而ELM的輸出層沒有誤差節點,也沒有上述過程 。
ELM使用嶺回歸求解輸出權重;SVM使用最大邊距最佳化(maximal margin optimization)給出結果。ELM可以直接求解多元分類(multiclass classification)的結果;而SVM通常分解為多次的二項分類(binary classification) 。ELM與SVM的學習精度相當,但ELM為達到這一精度所使用的學習時間更短 。
評價
在谷歌學術在2017年5月推出的“Classic Papers: Articles That Have Stood The Test of Time”測評活動中,與ELM有關的兩份研究被選入人工智慧領域持續受到引用的經典文獻 。
對ELM原創性的爭議
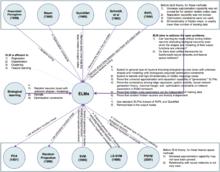 ELM與其它相關算法/概念間的關係。
ELM與其它相關算法/概念間的關係。機器學習領域有許多與ELM思路相當的算法,例如隨機向量連線函式 (Random Vector Functional-Link, RVFL)和Schmidt等 對前饋神經網路權重的隨機化實驗。因此,在ELM被提出後有觀點認為,ELM不是一種獨立的算法 。並且有評論指出,ELM原作者為了凸顯其工作的獨立性而有意迴避了對其它類似研究的引用 。但也有觀點認為,隨著研究的進行,ELM已發展為包含系統理論且與許多機器學習方法密切聯繫的學習系統,其作為獨立算法的存在已經成為事實 。
套用
ELM在許多領域都有套用,這裡提供一些個例作為介紹。在圖像處理方面,ELM被成功用於低解析度至高解析度圖像的轉化 ,以及遙感圖像中對下墊面類型的識別 。在生物科學領域,ELM被用於預測蛋白質互動作用 。地球科學領域的很多預測問題包含非線性過程且觀測數據缺乏,ELM因其良好的泛化能力而得到套用,成功的例子包括對日河流徑流量 、風速 和乾旱指數 的預測。
包含ELM算法的編程模組
HP-ELM :該模組是基於Python開發的ELM算法庫,包含GPU加速和記憶體最佳化設計,適用於處理大數據問題。HP-ELM支持LOO(Leave One Out)和分組交叉驗證(k-fold cross validation)動態選擇隱含層節點個數,可用的特徵映射包括線性函式、Sigmoid函式、雙曲正弦函式和三種徑向基函式。
ELM原作者Guang-Bin Huang的個人主頁上有ELM原始碼開放下載 。