定義
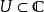 全純函式
全純函式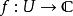 全純函式
全純函式 全純函式
全純函式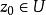 全純函式
全純函式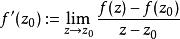 全純函式
全純函式設開子集且 是一個單複變函數,稱在 ( 復) 可微( [complex] differentiable) 或全純,如果極限 存在。
 全純函式
全純函式 全純函式
全純函式 全純函式
全純函式 全純函式
全純函式 全純函式
全純函式若 在 中處處可微,則稱 在上 全純(holomorphic over)。
等價定義
一個單複變函數全純若且唯若它實可微並且滿足 Cauchy-Riemann 方程.
例子
 全純函式
全純函式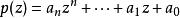 全純函式
全純函式 全純函式
全純函式所有關於 的復係數的多項式 函式在 上是全純的.
 全純函式
全純函式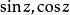 全純函式
全純函式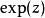 全純函式
全純函式所有關於 的三角函式 和指數函式 也是 (三角函式和指數函式通過歐拉公式聯繫).
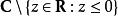 全純函式
全純函式對數函式的主支在集合 上全純. 平方根函式可以定義為
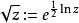 全純函式
全純函式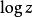 全純函式
全純函式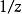 全純函式
全純函式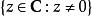 全純函式
全純函式所以任何複對數 全純的地方, 它也全純. 函式 在 上全純.
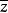 全純函式
全純函式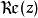 全純函式
全純函式不是全純的函式的典型例子有復共軛 (complex conjugation) 和取實部 .
性質
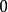 全純函式
全純函式因為復微分是線性的,並且服從積、商、鏈式法則,所以全純函式的和、積和複合是全純的,而兩個全純函式的商在所有分母非 的地方全純。
 全純函式
全純函式每個全純函式在每一點無窮可微。它和它自己的泰勒級數相等,而泰勒級數在每個完全位於定義域 內的開圓盤上收斂。泰勒級數也可能在一個更大的圓盤上收斂;例如,對數的泰勒級數在每個不包含0的圓盤上收斂,甚至在復實軸的附近也是如此。證明請參看全純函式解析。
全純函式滿足Cauchy-Riemann方組,該方程組含有兩個偏微分方程,也可以用復偏導運算元寫成一個。
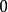 全純函式
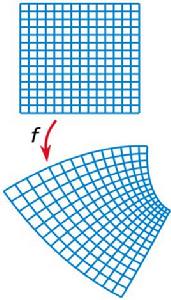
全純函式在非 導數的點的附近,全純函式是共形的 (或保角的,實際上就是相似在局部的推廣)。因為它保持了圖形的局部角度和形狀 (但尺寸可能改變)。
Cauchy 積分公式表明每個全純函式在圓盤內的值由它在盤邊界上的取值所完全決定。
幾個變數
多復變數的復解析函式定義為在一點全純和解析,如果它局部可以(在一個多盤,也即中心在該點的圓盤的直積)擴張為收斂的各個變數的冪級數。這個條件比Cauchy-Riemann方程要強。事實上它可以這樣表述:
一個多復變數函式是全純的若且唯若它滿足Cauchy-Riemann方程並且局部平方可積。
擴展到泛函分析
全純函式的概念可以擴展到泛函分析中的無窮維空間。Fréchet導數條目介紹了巴拿赫空間上的全純函式的概念。