定義
設f是定義在可測集E上的實函式。如果對每一個實數,集E[f>a]恆可測(勒貝格可測),則稱f是定義在 E上的(勒貝格)可測函式。
定理 設f是定義在可測集E上的實函式,下列任一個條件都是在E上(勒貝格)可測的充要條件:
(1) 對任何有限實數a,E[f>=a]都可測;
(2) 對任何有限實數a,E[f<a]都可測;
(3) 對任何有限實數a,E[f=<a]都可測;
(4) 對任何有限實數a,b,E[a=<f<b]都可測。
設(X,F)為一可測空間,E是一個可測集。f: E→R*為定義在E上的函式。若對任意實數a,總有{x∈E: f(x)<a}∈F,則稱f為E上的F-可測函式(簡稱E上的可測函式)。
特別地,若可測空間取為是R 上的Lebesgue可測空間。E是R 中的Lebesgue可測集。則E上的可測函式成為Lebesgue可測函式。若可測空間取為R 上的Borel可測空間,E是R 中的Borel集,則E上的可測函式稱為Borel可測函式。
特殊函式
如果( X, Σ)和( Y, Τ)是波萊爾空間,則可測函式 f又稱為波萊爾函式。所有連續函式都是波萊爾函式,但不是所有波萊爾函式都是連續函式。然而,可測函式幾乎是連續函式;參見盧辛定理。
根據定義,隨機變數是定義在樣本空間上的可測函式。
性質
(1)兩個可測的實函式的和與積也是可測的。
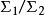 可測函式
可測函式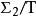 可測函式
可測函式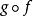 可測函式
可測函式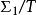 可測函式
可測函式(2)如果函式 f是可測的,函式 g是可測的,那么複合函式是可測的。
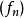 可測函式
可測函式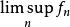 可測函式
可測函式(3)可數個可測函式的最小上界也是可測的。如果是一個可測函式序列,在[−∞,+∞]中取值,那么也是可測的。
(4)可測函式的逐點極限是可測的。(連續函式的對應命題需要比逐點收斂更強的條件,例如一致收斂。)
(5)只有可測函式可以進行勒貝格積分。
(6)一個 勒貝格可測函式是一個實函式 f: R→ R,使得對於每一個實數 a,集合
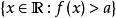 可測函式
可測函式都是勒貝格可測的集合。勒貝格可測函式的一個有用的特徵,是f是可測的若且唯若mid{-g,f,g}對於所有非負的勒貝格可積函式g都是可積的。
不可測函式
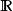 可測函式
可測函式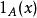 可測函式
可測函式不是所有的函式都是可測的。例如,如果A是實數軸的一個不可測子集,那么它的指示函式是不可測的。

