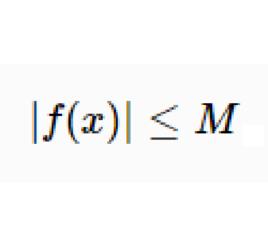定義
定義1
 有界
有界 有界
有界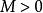 有界
有界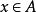 有界
有界設函式在數集上有定義,如果存在常數,使得對任意,有
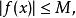 有界
有界 有界
有界 有界
有界則稱函式在數集上 有界,否則稱為 無界。
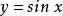 有界
有界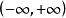 有界
有界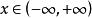 有界
有界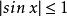 有界
有界例如,函式在其定義域內有界,這是因為對任意,總有。
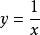 有界
有界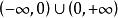 有界
有界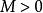 有界
有界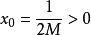 有界
有界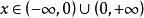 有界
有界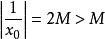 有界
有界 有界
有界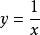 有界
有界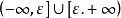 有界
有界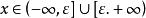 有界
有界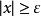 有界
有界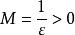 有界
有界 有界
有界再如,函式在其定義域內是無界的,這是因為對任意的實數,總存在點,顯然,使得,然而,對任意實數,函式在定義域的子集上卻是有界的,這是因為對任意,總有,於是便可取實數.使得。
定義2
 有界
有界 有界
有界 有界
有界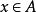 有界
有界設函式在數集上有定義,如果存在常數,使得對任意,有
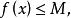 有界
有界 有界
有界 有界
有界 有界
有界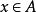 有界
有界則稱函式在數集上 有上界,並稱M為在A上的 上界.如果存在常數m,使得對任意,有
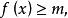 有界
有界 有界
有界 有界
有界 有界
有界 有界
有界則稱函式在數集上 有下界,並稱m為在上的 下界。
 有界
有界 有界
有界 有界
有界 有界
有界顯然,若在A上有界,則在A必有上、下界,反之,若在A上有上、下界,則在A上必有界。
 有界
有界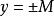 有界
有界由定義1可知,在集合A上有界函式的圖形在A上,應介於平行於x軸的兩條直線之間,如圖1所示。
 圖1
圖1注意點
關於函式的有界性.應注意以下兩點:
(1)函式在某區間上不是有界就是無界,二者必屬其一;
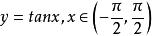 有界
有界(2)從幾何學的角度很容易判別一個函式是否有界(見圖2).如果找不到兩條與x軸平行的直線使得函式的圖形介於它們之間,那么函式一定是無界的,如。
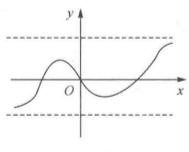 圖2
圖2例題解析
例1:討論下列函式的有界性:
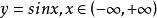 有界
有界(1);
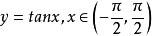 有界
有界(2).
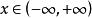 有界
有界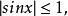 有界
有界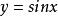 有界
有界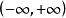 有界
有界解: (1)由於對一切,都有故在上是有界函式。
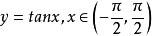 有界
有界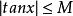 有界
有界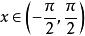 有界
有界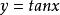 有界
有界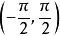 有界
有界(2)根據的圖形(見圖3)容易看出,不論正數M多么大,不等式不可能對一切均成立,因此在上是無界函式。
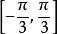 有界
有界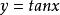 有界
有界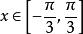 有界
有界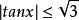 有界
有界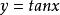 有界
有界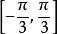 有界
有界但如果在區間上討論函式,因對一切,不等式成立,故在區間上是有界函式。
例2:
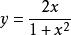 有界
有界證明:函式是有界函式。
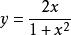 有界
有界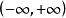 有界
有界證明:的定義域為,又
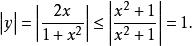 有界
有界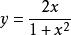 有界
有界因此是有界函式。