有界完全統計量

有界完全統計量(boundedly complete statistic)是常用的一類完全統計量，設(X，BX，P)是一個統計結構，其中P=Pθ：θ∈Θ，如果對於BX可測的有界函式φ(X)，由ᗄθ∈Θ，有Eθφ(X)=0，可推出φ(X)=0，a.s. 對P中任一分布成立，則稱此統計結構為有界完全(備)的，或稱分布族P是有界完全(備)的，如果統計量t(X)的誘導統計結構(T，BT，P)是有界完全的，則稱統計量t(X)是有界完全統計量 。

定義

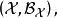有界完全統計量

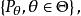有界完全統計量

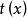有界完全統計量

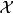有界完全統計量

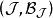有界完全統計量

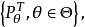有界完全統計量

設變數X的樣本空間為分布族為為定義於取值於的統計量，其分布族為若對任何滿足條件

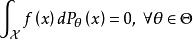有界完全統計量

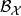有界完全統計量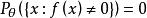

有界完全統計量

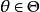有界完全統計量

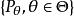有界完全統計量

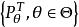有界完全統計量

有界完全統計量

有界完全統計量

的有界 可測函式，必有對一切，則稱分布族為 有界完全的.若為 有界完全的，則稱為 有界完全統計量 。

相關結論及定理

顯然， 完全的分布族或統計量必為有界完全的，下面的例子說明，此事實之逆不成立 。

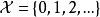有界完全統計量

例1設，分布族為

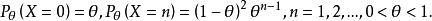有界完全統計量

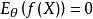有界完全統計量

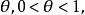有界完全統計量

設對一切則

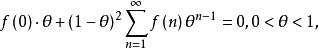有界完全統計量

即

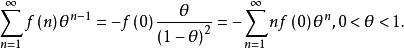有界完全統計量

有界完全統計量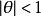

有界完全統計量

此式兩邊為的冪級數，在內收斂，故其對應項係數必相同，即

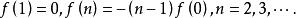有界完全統計量

有界完全統計量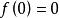

有界完全統計量

若要求有界，則由此知必須有，因而

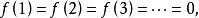有界完全統計量

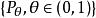有界完全統計量

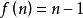有界完全統計量

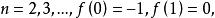有界完全統計量

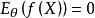有界完全統計量

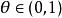有界完全統計量

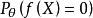有界完全統計量

這證明了為有界完全的。但它不為完全，因若取，當則易見對一切，但並不為1。

關於有界完全性有下面有趣的定理。

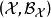有界完全統計量

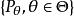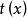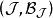有界完全統計量

有界完全統計量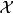

有界完全統計量

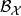有界完全統計量

有界完全統計量

有界完全統計量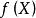

有界完全統計量

有界完全統計量

有界完全統計量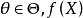

有界完全統計量

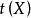有界完全統計量

定理1 設X的樣本空間和分布族為及，而為一有界完全統計量，取值於內，且為 充分統計量，則對任何定義於的有限-可測函式，當的分布與無關時,對一切與獨立。

值得注意的是: 本定理之逆不真。

由於指數族有完全(因而有界完全)和充分的統計量，故由以上定理得到:

系1 設X的分布族為指數族

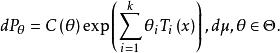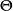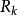有界完全統計量

有界完全統計量

有界完全統計量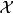

有界完全統計量

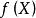有界完全統計量

有界完全統計量

有界完全統計量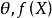

有界完全統計量

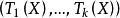有界完全統計量

而作為的子集有內點：則對任何(定義於且取值於某可測空間)，當的分布與無關時，對任何必與獨立(在這個具體情況下可以證明，上述事實之逆亦真) 。