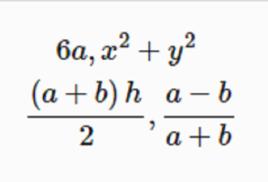定義
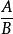有理式
有理式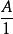有理式指可以將多項式A和多項式B用 的形式表示的式子。因為多項式A可以用 表示，所以 多項式也可以稱為有理式。在有理式中，不是多項式的式子稱為 分式，有理式包含多項式和分式。
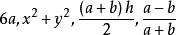有理式
有理式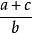
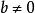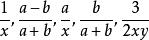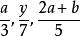有理式
有理式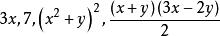
有理式
有理式代數式根據它所包含的運算可以分為有理式和無理式，而有理式又可以分為整式和分式。我們把只含有加、減、乘、除和乘方這五種運算的代數式叫做 有理代數式，簡稱 有理 式。例如等都是有理式，類似分數的叫法，我們把這樣的代數式叫做分式()．對於分式，我們規定，分子可以是一個確定的數，也可以是一個式子，但分母卻必須是一個含有字母的式子，而不能是一個確定的數。例如等都是分式，而等都不是分式。從形式上看，凡是分母中含有字母的有理式叫做 有理分式，簡稱 分式，相對於分式，把分母中不含有字母或不包含除法運算的有理式叫做 有理整式，簡稱 整式。例如等都是整式。
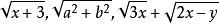有理式含有關於字母開方運算的代數式稱為無理式。例如等。
有理式的性質
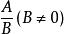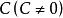有理式
有理式有關於多項式A，B的分式 ，當 為多項式時，下列式子成立：
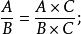有理式(1)
有理式(2)
有理式(3)
有理式(4)
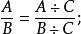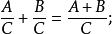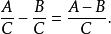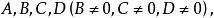有理式另外，關於多項式 下列式子也成立：
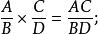有理式(1)
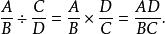有理式(2)
有理式的計算
分式的分子、分母同時乘以或除以不為0的相同的多項式，分式的值不變。分式的分母和分子除以它們的公約數，使之最簡化的過程叫作 約分，分式中的約分也和數的約分相同，無法再進行約分的分式叫作 最簡分式。
將分式化為最簡分式
如果分式的分母、分子都是單項式，則將分式的分母、分子同時除以公約數，轉化成最簡分式。如：
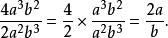有理式如果分式的分母、分子都是多項式，則將分式的分母、分子分解因式後除以公因式，轉化成最簡分式。如：
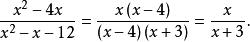有理式分式的加減乘除
使兩個以上的分式中的分母相同的過程叫作 通分 。和分數一樣，要將分式進行通分，則需要將分母的最低公倍式轉化成分式的公分母，通過比較分數和分式之間的差異來解題，就可以更輕鬆地得出答案。
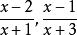有理式
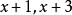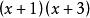有理式
有理式例如，要將分式 進行通分，兩個分式的分母 的最低公倍式為 ，所以將兩式進行通分，可得
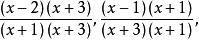有理式從而使兩個分式的加減運算變得簡便。
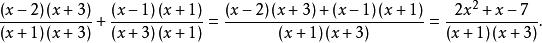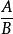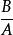有理式 有理式
有理式與有理數相同，當兩個有理式的積為1時，我們把一個式子叫作另一個式子的 倒數。例如，有理式的倒數為。因此，把除以某個有理式轉化為乘以這個有理式的倒數的運算顯得更為簡單。
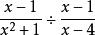有理式例如，計算時，轉化為乘以倒數後再進行計算。
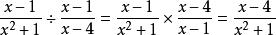有理式即。像這樣，在計算分式的除法時，根據分數的計算方法進行思考就更簡單了。
