第一型
定義
 曲面積分
曲面積分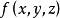 曲面積分
曲面積分 曲面積分
曲面積分 曲面積分
曲面積分 曲面積分
曲面積分 曲面積分
曲面積分 曲面積分
曲面積分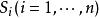 曲面積分
曲面積分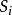 曲面積分
曲面積分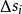 曲面積分
曲面積分 曲面積分
曲面積分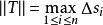 曲面積分
曲面積分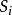 曲面積分
曲面積分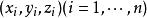 曲面積分
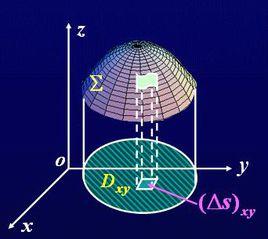
曲面積分設 為空間中的曲面, 為定義在 上的函式.對曲面作分割 ,它把分成 個可求面積的小曲面片 , 的面積記為 ,分割 的細度為 ,在 上任取一點 , 若存在極限
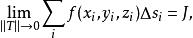 曲面積分
曲面積分 曲面積分
曲面積分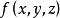 曲面積分
曲面積分 曲面積分
曲面積分且它的值與分割及點的取法無關,則稱此極限 為 在 上的 第一型曲面積分 ,記為
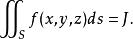 曲面積分
曲面積分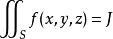 曲面積分
曲面積分或者簡寫成 。
第一型曲面積分的計算
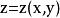 曲面積分
曲面積分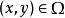 曲面積分
曲面積分 曲面積分
曲面積分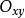 曲面積分
曲面積分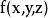 曲面積分
曲面積分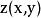 曲面積分
曲面積分 曲面積分
曲面積分設空間曲面S的方程為 , ,其中 為曲面S在 平面上的投影域,函式 在曲面S上連續,如果 在 上有連續的一階偏導數,則有
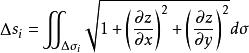 曲面積分
曲面積分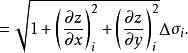 曲面積分
曲面積分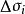 曲面積分
曲面積分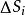 曲面積分
曲面積分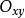 曲面積分
曲面積分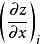 曲面積分
曲面積分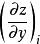 曲面積分
曲面積分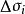 曲面積分
曲面積分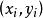 曲面積分
曲面積分其中 是 在 上的投影域, 和 表示在 內某點 處的兩個偏導數。由第一型曲面積分的定義,於是將第一型曲面積分化為二重積分的計算
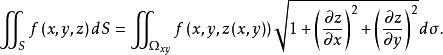 曲面積分
曲面積分物理意義
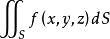 曲面積分
曲面積分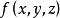 曲面積分
曲面積分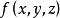 曲面積分
曲面積分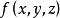 曲面積分
曲面積分表示以 為面密度的空間曲面S的“質量”,即將空間曲面S想像成一塊光滑的(可微的)不摺疊的(單值的)質量分布服從 的薄板,故 在S上的第一型曲面積分就是薄板的代數質量 。
第二型
 曲面積分
曲面積分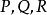 曲面積分
曲面積分 曲面積分
曲面積分 曲面積分
曲面積分 曲面積分
曲面積分 曲面積分
曲面積分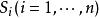 曲面積分
曲面積分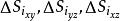 曲面積分
曲面積分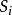 曲面積分
曲面積分 曲面積分
曲面積分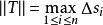 曲面積分
曲面積分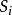 曲面積分
曲面積分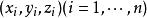 曲面積分
曲面積分設 為空間中的曲面, 為定義在 上的函式.對曲面作分割 ,它把分成個可求面積的小曲面片 , 分別代表 在三個坐標面的投影面積。分割的細度為 ,在 上任取一點 , 若存在極限
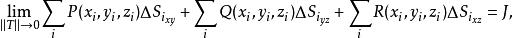 曲面積分
曲面積分 曲面積分
曲面積分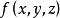 曲面積分
曲面積分 曲面積分
曲面積分且它的值與分割及點的取法無關,則稱此極限 為 在 上的 第二型曲面積分 ,記為
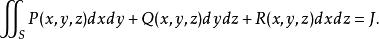 曲面積分
曲面積分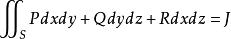 曲面積分
曲面積分或者簡寫成 。
第二型曲面積分的計算
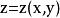 曲面積分
曲面積分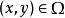 曲面積分
曲面積分 曲面積分
曲面積分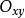 曲面積分
曲面積分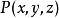 曲面積分
曲面積分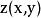 曲面積分
曲面積分 曲面積分
曲面積分設空間曲面S的方程為 , ,其中 為曲面S在 平面上的投影域,函式 在曲面S上連續,如果 在 上有連續的一階偏導數,則有
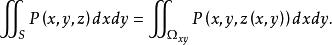 曲面積分
曲面積分物理意義
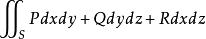 曲面積分
曲面積分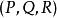 曲面積分
曲面積分 曲面積分
曲面積分表示以為空間流體的流速場,單位時間流經曲面的總流量 。