積分輪換對稱性特點及規律
(1) 對於曲面積分，積分曲面為u(x,y,z)=0，如果將函式u(x,y,z)=0中的x,y,z換成y,z,x後，u(y,z,x)仍等於0，即u(y,z,x)=0， 也就是積分曲面的方程沒有變，那么在這個曲面上的積分 ∫∫f(x,y,z)dS=∫∫f(y,z,x)dS；如果將函式u(x,y,z)=0中的x,y,z換成y,x,z後，u(y,x,z)=0，那么在這個曲面上的積分 ∫∫f(x,y,z)dS=∫∫f(y,x,z)dS；如果將函式u(x,y,z)=0中的x,y,z換成z,x,y後，u(z,x,y)=0，那么在這個曲面上的積分 ∫∫f(x,y,z)dS=∫∫f(z,x,y)dS ，同樣可以進行多種其它的變換。
(2) 對於第二類曲面積分只是將dxdy也同時變換即可 ，比如：如果將函式u(x,y,z)=0中的x,y,z換成y,z,x後，u(y,z,x)=0，那么在這個曲面上的積 分 ∫∫f(x,y,z)dxdy=∫∫f(y,z,x)dydz,∫∫f(x,y,z)dydz=∫∫f(y,z,x)dzdx, ∫∫f(x,y,z)dzdx=∫∫f(y,z,x)dxdy。
(3) 將(1)中積分曲面中的z去掉，就變成了曲線積分滿足的輪換對稱性:積分曲線為u(x,y)=0，如果將函式u(x,y)=0中的x,y換成y,x後，仍滿足u(y,x)= 0，那么在這個曲線上的積分 ∫f(x,y)ds=∫f(y,x)ds；實際上如果將函式u(x,y)=0中的x,y換成y,x後，仍滿足u(y,x)=0，則意味著積分曲線關於直線y=x對稱 。第二類三維空間的曲線積分跟（2）總結相同同。但第二類平面上的曲線積分不同∫f(x,y)dx=-∫f(y,x)dy.(注意前面多了一個負號）
(4) 二重積分和三重積分都和(1)的解釋類似，也是看積分域函式將x,y,z更換順序後，相當於將坐標軸重新命名，積分區間沒有發生變化，則被積函式作相應變換後，積分值不變。
二重積分的輪換對稱性
定理1 設函式f(x,y)在有界閉域D上連續,D對坐標x,y具有輪換對稱性 ,則
積分輪換對稱性三重積分的輪換對稱性
定理2:設函式f(x,y,z)在有界閉域Ω上連續,Ω對坐標x,y,z具有輪換對稱性 ,則
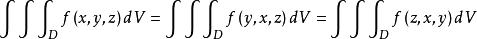積分輪換對稱性第一型曲線積分的輪換對稱性
定理3 設L是xoy面上的一條光滑或分段光滑的曲線弧,L對坐標x,y具有輪換對稱性,f(x,y)在L上連續,則
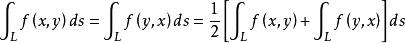積分輪換對稱性第二型曲線積分的輪換對稱性
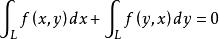積分輪換對稱性定理4 設L是xoy面上的一條光滑或分段光滑的有向曲線弧,L對坐標x,y具有輪換對稱性,f(x,y)在L上連續,則
第一型曲面積分的輪換對稱性
定理5 設∑是光滑或分片光滑的曲面,∑對坐標x,y,z具有輪換對稱性,f(x,y,z)在∑上連續,則
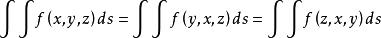積分輪換對稱性第二型曲面積分的輪換對稱性
定理6 設∑是光滑或分片光滑的有向曲面,∑對坐標x,y,z具有輪換對稱性,f(x,y,z)在∑上連續,則
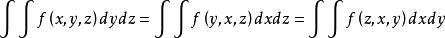積分輪換對稱性