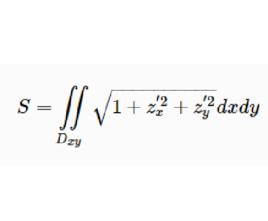曲面面積

曲面面積(area of a surface)是指曲面表面的面積。把光滑曲面S分成沒有公共內點的n塊S1,... , Sn，且每一塊仍是光滑曲面，在每個S上取一點P，過P作S的切平面T，將s投影到T上，所有這些投影的面積之和的極限(當所有S的直徑趨於零時)如果存在，就是曲面S的面積，對有界簡單光滑曲面而言，這樣的極限總是存在的，而且與曲面的光滑等價的參數表示的選擇無關。

基本介紹

曲面面積

設空間有界曲面 為

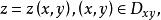曲面面積

曲面面積

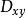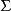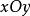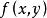曲面面積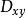

曲面面積

曲面面積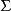

曲面面積

曲面面積

其中 是 在 面上的投影區域， 在 上具有連續的偏導數，下面討論曲面的面積的計算問題。

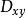曲面面積

曲面面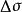積

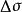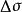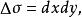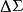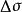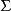曲面面積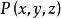

曲面面積

曲面面積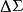

曲面面積

曲面面積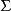

曲面面積

曲面面積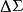

曲面面積

曲面面積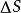

曲面面積

曲面面積

現用平行於x軸和y軸的兩組平行直線分割投影區域 ，如圖1所示，任取其中的一塊記作 ，其面積也記作 ，則當 的直徑很小時， 表示以 的邊界為準線，母線平行於z軸的柱面截得的曲面 上的那部分，設 是 上的任一點，根據條件，曲面 在點P處有切平面，則可用柱面截得切平面上的那一小片平面的面積dS近似地代替 的面積 ，則

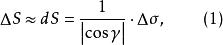曲面面積

曲面面積

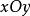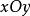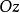曲面面積

曲面面積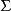

曲面面積

曲面面積

其中， 是切平面與 面的夾角，也就是切平面的法向量 n與 面的法線 軸的夾角，由曲面 的方程可知

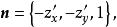曲面面積

所以

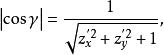曲面面積

代人式(1)得

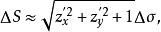曲面面積

則曲面的面積微元為

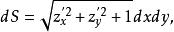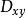曲面面積

曲面面積

將dS在投影區域 上積分，便得計算曲面面積的二重積分公式

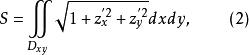曲面面積

曲面面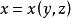積

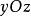曲面面積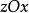

曲面面積

曲面面積

如果所求曲面的方程用 或 表示比較方便，則同理可將曲面分別投影到 面或 面，類似地可得相應曲面的面積計算公式，分別為

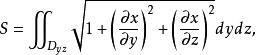曲面面積

或

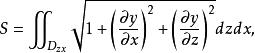曲面面積

曲面面積

曲面面積

其中， 分別為曲面 在yOz面或zOx面上的投影區域。

例題解析

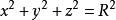曲面面積

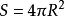曲面面積

例1 證明球面 的表面積為。

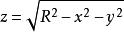曲面面積

解: 由對稱性，取上半球面方程為 ，它在xOy面上的投影區域為

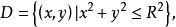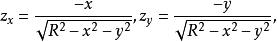曲面面積

曲面面積

由式（2）得

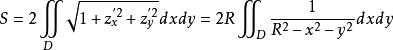曲面面積

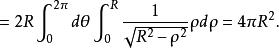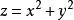曲面面積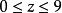

曲面面積

曲面面積

例2 求拋物面位於之間的那一部分的面積。

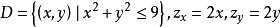曲面面積

解: 曲面在xOy面上的投影區域，由式(2)，得

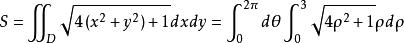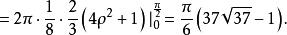曲面面積

曲面面積