定理定義
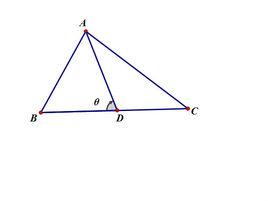
設已知△ABC及其底邊上B、C兩點間的一點D,則有:
AB²·DC+AC²·BD-AD²·BC=BC·DC·BD。
驗證推導
證法一
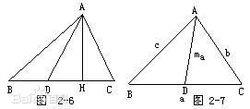
已知:如圖2-6所示,在△ABC中,點D是線段BC上的一點,連線AD。
求證:AB²·DC+AC²·BD-AD²·BC=BC·DC·BD。
證明:如圖2-6所示,作AH⊥BC於H。為了明確起見,設H和C在點D的同側。
由廣勾股定理 有:
 斯特瓦爾特定理
斯特瓦爾特定理AC²=AD²+DC²-2DC·DH······(1)
AB²=AD²+BD²+2BD·DH······(2)
用BD乘(1)式兩邊得:
AC²·BD=AD²·BD+DC²·BD-2DC·DH·BD······(3)
用DC乘(2)式兩邊得:
AB²·DC=AD²·DC+BD²·DC+2BD·DH·DC······(4)
由 (3)+(4) 得到:
AC²·BD+AB²·DC
=AD²·(BD+DC)+DC²·BD+BD²·DC
=AD²·BC+BD·DC·BC
∴AB²·DC+AC²·BD-AD²·BC=BC·DC·BD
證法二
已知:如圖2-6所示,在△ABC中,點D是線段BC上的一點,連線AD。
求證:AB²·DC+AC²·BD-AD²·BC=BC·DC·BD。
證明:
∵∠BDA+∠CDA=180°
∴cos∠BDA+cos∠CDA=0
根據餘弦定理得:
AB²=BD²+AD²-2BD·AD·cos∠BDA······(1)
AC²=CD²+AD²-2CD·AD·cos∠CDA······(2)
用CD乘(1)式兩邊得:
AB²·CD=BD²·CD+AD²·CD-2BD·AD·CD·cos∠BDA
用BD乘(4)式兩邊得:
AC²·BD=CD²·BD+AD²·BD-2CD·AD·BD·cos∠CDA
由 (3)+(4) 得到:
AB²·CD+AC²·BD
=BD²·CD+AD²·CD-2BD·AD·CD·cos∠BDA+CD²·BD+AD²·BD-2CD·AD·BD·cos∠CDA
=(BD²·CD+CD²·BD)+(AD²·CD+AD²·BD)-(2BD·AD·CD·cos∠BDA+2CD·AD·BD·cos∠CDA)
=BD·CD·(BD+CD)+AD²·(CD+BD)-2BD·AD·CD·(cos∠BDA+cos∠CDA)
=BD·CD·BC+AD²·CD-2BD·AD·CD·0
=BD·CD·BC+AD²·CD
∴AB²·DC+AC²·BD-AD²·BC=BC·DC·BD。
斯特瓦爾特定理的逆定理成立。
定理推廣
斯特瓦爾特定理還有如下推論:
在△ABC中,點D是線段BC上的一點,連線AD。
(1)若AB=AC,則AD²=AB²-BD·DC;
(2)若AD為BC中線,則AD²=1/2(AB²+AC²)-1/4BC² (即中線定理);
(3)若AD為∠BAC內角平分線,則AD²=AB·AC﹣BD·DC (即角平分線長公式);
(4)若AD為∠BAC外角平分線,則AD²=﹣AB·AC+BD·DC;
(5)若BD/BC=λ,則AD²=λ·(λ﹣1)·BC²+(1﹣λ)·AB²+λ·AC²。
並且斯特瓦爾特定理與托勒密定理和張角定理可以互化。
常見套用
①用於得到線段倍份關係;
②用於求解三角形問題(選擇適當的三角形及其邊上的點;靈活運用推論)。