基本介紹
定義
 斜坐標系
斜坐標系 斜坐標系
斜坐標系 斜坐標系
斜坐標系 斜坐標系
斜坐標系所謂斜坐標系就是以平面內任意兩個不共線矢量 、 所在的直線為 軸、 軸,建立如圖(1)所示的斜坐標系 ,
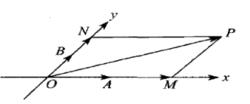 圖1
圖1 斜坐標系
斜坐標系 斜坐標系
斜坐標系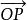 斜坐標系
斜坐標系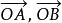 斜坐標系
斜坐標系其中矢量 稱為該斜坐標系的單位矢量,它們的夾角 ,O為坐標原點,則由平面矢量基本定理可知:對於該平面內任意給定的矢量 可以表示為單位矢量 的線性疊加,而且這種表達式是唯一的,即
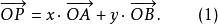 斜坐標系
斜坐標系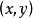 斜坐標系
斜坐標系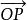 斜坐標系
斜坐標系為了表述方便,這裡有序實數對 被分別定義為矢量 在斜坐標軸的坐標,也可以稱作是該矢量在兩坐標軸上的投影。
相關性質
和直角坐標系一樣,矢量在斜坐標系中同樣具有如下主要性質:
性質1:在如圖1所示的斜坐標系中,點O、A、B的坐標分別表示為(0,0);(1,0);(0,1)。
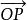 斜坐標系
斜坐標系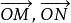 斜坐標系
斜坐標系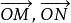 斜坐標系
斜坐標系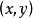 斜坐標系
斜坐標系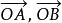 斜坐標系
斜坐標系 斜坐標系
斜坐標系性質2:由矢量平行四邊形法則可知:任意矢量 都可以沿坐標軸分解為 ,且 與P的坐標 和單位矢量 滿足關係式 。
注意事項
首先,應該根據物理問題情境,尤其是根據初始條件建立恰當的斜坐標系。我們必須清楚:利用直角坐標系主要是為了簡化數學處理過程;而斜坐標系主要是為簡化物理過程而引入的,例如在處理質點平面運動的時候,雖說斜坐標系有時會獲得一舉雙得的效果,既能直接還原物理本質,又能簡化問題處理過程; 但是在具體使用時,必須知道斜坐標系的使用方法和注意事項,其中每一條軸儘可能代表質點的某一具體的運動形式,例如勻速直線運動,自由落體運動、勻變速直線運動等。其次,在斜坐標系中,不同軸所代表的質點運動形式是相互獨立的。最後,在斜坐標系中,不但質點的平面運動的合成與分解,而且矢量的運算法則均和直角坐標系中的情形完全一樣,比如平行四邊形法則;三角形法則;正玄定理和餘弦定理等。
套用舉例
下面我們通過具體實例來體會 利用斜坐標系處理部分質點平面運動中的優勢。
 斜坐標系
斜坐標系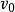 斜坐標系
斜坐標系 斜坐標系
斜坐標系實例:如圖2所示,在傾角 為的斜坡坡底處,以初速度 、與斜面夾角為 的方向拋射物體,求物體在斜面上的射程。
 圖 2
圖 2為了集中體現斜坐標系在處理類似問題中的作用,我們不妨用直角坐標系的和斜坐標系兩種方法來解決這個問題。
 斜坐標系
斜坐標系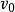 斜坐標系
斜坐標系 斜坐標系
斜坐標系 斜坐標系
斜坐標系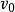 斜坐標系
斜坐標系解: ( 斜坐標系法)我們可以以拋出時為初始時刻建立如圖3所示的二維斜坐標系,其中軸的方向與方向一致,軸與重力加速度的方向一致。在該斜坐標系中,質點的平面運動是由沿方向的勻速直線運動和沿重力方向的自由落體運動合成的。
 斜坐標系
斜坐標系如圖3所示,設物體在斜面上的射程為OA,從拋出點o開始,經過時間t後,物體落到斜面上A點。在軸,物體發生的位移為:
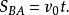 斜坐標系
斜坐標系在y軸,時間t物體走過的位移為:
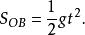 斜坐標系
斜坐標系 斜坐標系
斜坐標系通過位移矢量三角形可以求解物體在斜面上的射程OA.具體如下:
 斜坐標系
斜坐標系在中,由幾何關係可知,
 斜坐標系
斜坐標系由正弦定理可知:
 斜坐標系
斜坐標系即:
 斜坐標系
斜坐標系由首末兩項可求得時間:
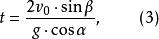 斜坐標系
斜坐標系把(3)式代入(2)中,再次利用(2)式的第二項和第三項,可以解出物體在斜面上的射程
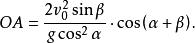 斜坐標系
斜坐標系斜坐標系最明顯的特點是 每一個坐標軸代表質點的最基本的運動形式,例如勻速直線運動,自由落體運動等;其次,該方法充分利用矢量性質和數學定理。基於這些,斜坐標系法具有計算簡單,理解容易,過程直接等特點。
評析: 在質點的平面運動教學中,斜坐標系處理方法的作用不僅僅局限於上述情形,上面的例子只是窺豹一斑,掛一漏萬,不足以說明教學的全部,但是通過前述實例可以看出有時採用斜坐標系可以實現如下主要教學效果。
1. 在質點平面運動中,適時巧妙的引入斜坐標系有利於簡化物理過程斜坐標系相比直角坐標系沒有本質上的不同,只是在處理質點的平面運動時,斜坐標系在對運動分解後的運動形式更為直接、簡單。從例子可以看出來,在斜坐標系中,可以把質點的運動分解為最簡單的勻速直線運動和最基本的初速為零的勻加速直線運動;而在直角坐標系中,兩個坐標軸上的分運動依然是初速不為零的勻變速直線運動,這樣一來,斜坐標系方法可以大大簡化處理過程。
2. 有時利用斜坐標系處理問題,有利於加深對矢量的性質、數學定理的理解和運用在用斜坐標系方法處理運動學問題時,必須對矢量的平移不變性這一性質有較深的認識和理解,同時依據平移不變性,要具備善於巧妙構建矢量三角形的能力;此外,從數學角度而言,要求能熟練地運用正弦定理處理物理問題,所有這些要求無疑會提高解決物理問題的綜合素質。
3. 斜坐標系方法的引入有利於培養的創新思維。面對質點平面運動問題時,絕大部分人習慣於、甚至依賴於直角坐標系(這當然不失為一種方法),如果能根據實際巧妙的引入斜坐標系,這種另闢蹊徑的方法定會使思維耳目一新、面對新的物理問題情境會變得豁然開朗、迎刃而解;潛移默化中,創新思維會得到極大地鍛鍊和提升。

