定義
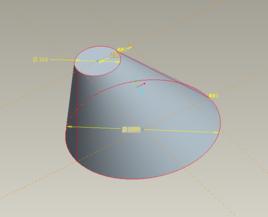
斜圓錐就是底面為圓形而且任意一個平行於底面且與之相交的平面與斜圓錐的截面都是圓形（在頂點處的截面可以視為是退化的半徑為0的圓），而且這些截面圓的圓心都在底面中心O到頂點V的連線上的立體圖形。
一般需要三個參數來確定斜圓錐的形狀：底面半徑r，底面中心O與頂點V的連線（不妨稱為是中軸線）的長度L，以及頂點位矢與底面的法向量（方向為指向頂點的一側）的有向交角的正切k（這個參數不妨稱為傾斜度）
過斜圓錐的頂點作它與底面邊緣的連線，可以發現連線的長度在兩個點P1,P2上分別取最大值和最小值，如果以底面中心為原點，垂直於底面且指向頂點的一側的方向為z軸正方向，向量P1P2的方向為x軸正方向，建立空間直角坐標系，那么斜圓錐面的方程可以寫為
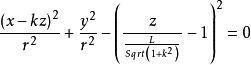斜圓錐
斜圓錐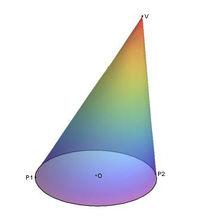性質
斜圓錐面是可展曲面，但是其展開圖的方程卻異常複雜，同樣不難料到的是，斜圓錐的側面的面積是關於r，k，L的十分複雜的函式，具體來說是十分複雜的積分，即使使用Maple和Mathematica這樣的數學軟體都難以得到封閉形式。
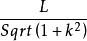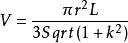斜圓錐
斜圓錐但是根據祖暅原理，參數為r，k，L的斜圓錐的體積與高為，底面半徑為r的正圓錐等效，所以可以給出斜圓錐體積的封閉形式：
展開角
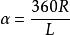斜圓錐在斜圓錐面的板金下料過程中· 會遇到確定其展開角度的問題。 對於正圓錐面，其展開角α可用展開後的中心角表示：
式中,R為圈錐的底圓半徑,L為圓錐素線的實長。而對於斜圓錐面， 預先確定其展開角是比較困難的。 從數學上看，斜圓錐面的展開角可表達成橢圓積分的形式， 而這個積分用普通方法解是不出來的。經分析和研究，採用了圖解計算法來解決這一問題， 並利用計算機來進行計算， 然後將計算結果繪製成曲線圖。 事實證明，這種方法簡便可行，並且是實用的。
