定義
質心是描述質點系整體運動狀態的代表點。質點系中每一個質點既與質心一起運動,又有相對於質心的運動.各個質點運動狀態的差異。表現為相對於質心有不同的速度。
所謂各個質點相對於質心的運動,就是各個質點相對於質心坐標系的運動.所謂質心坐標系,可以形象地規定為以質心為原點(參考點),並且坐標軸指向固定方向的平動參考系,簡稱質心繫.如果質點系是孤立系統,則它的質心繫是慣性系;否則,不一定是慣性系。
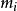 質心坐標系
質心坐標系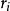 質心坐標系
質心坐標系 質心坐標系
質心坐標系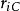 質心坐標系
質心坐標系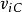 質心坐標系
質心坐標系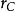 質心坐標系
質心坐標系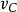 質心坐標系
質心坐標系考慮由行個質點構成的質點系.以固定點O為基點建立慣性坐標系.設質點系內第i個質點P:質量為,相對於慣性系的徑矢為,速度為,相對於質心繫的位矢為,速度為,令該質點系的質心C相對於慣性系的徑矢為,速度,根據平動參考系的變換關係式,有
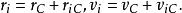 質心坐標系
質心坐標系於是由
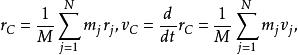 質心坐標系
質心坐標系可得
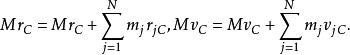 質心坐標系
質心坐標系由上式可得
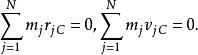 質心坐標系
質心坐標系上式的意義是:任何質點系在它的質心繫中的總動量為零矢量.或者說:任何質點系在它的質心繫申遵循動量守恆定律,不論質心繫是否受到外部的作用。顯然,質心繫是一種特殊的參考系。
套用
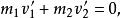 質心坐標系
質心坐標系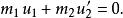 質心坐標系
質心坐標系下面我們套用質心坐標系來處理粒子的斜碰撞。當兩粒子不受外力作用,則兩粒子的質心相對於慣性系是作勻速直線運動,所以質心繫亦是慣性系,故在質心繫中動量、能量守恆定律亦成立。在質心繫中,兩粒子的總動量等於零,即在碰撞前有碰撞後亦有
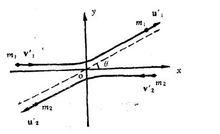 圖1:質心坐標系中的斜碰撞
圖1:質心坐標系中的斜碰撞 質心坐標系
質心坐標系於是就得出結論:在質心坐標系中,在碰撞前兩粒子以相反的方向入射而在碰撞後兩粒子以相反的方向出射,亦即在質心繫中,動量守恆定律要求兩個粒子的散射角是相等的,都等於。而根據動能守恆有
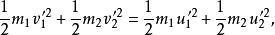 質心坐標系
質心坐標系以動量守恆定律代入,得
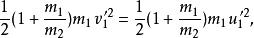 質心坐標系
質心坐標系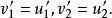 質心坐標系
質心坐標系 質心坐標系
質心坐標系 質心坐標系
質心坐標系 質心坐標系
質心坐標系所以有亦即在質心繫中,兩個粒子作非對心彈性碰撞,碰撞的結果是使每個粒子運動方向發生改變,但運動速率不變。至於粒子入射方向與出射方向的夾角,即散射角則單由動量守恆和能量守恆定律是不能確定的,散射角可以取從0到之間的任何值。
質心坐標系與實驗室坐標系的關係
由於在實際工作中容易測定的是在實驗室坐標系中的散射角而不是質心繫中的散射角,所以還必須建立起質心繫和實驗室系的關係。
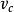 質心坐標系
質心坐標系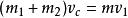 質心坐標系
質心坐標系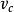 質心坐標系
質心坐標系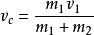 質心坐標系
質心坐標系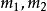 質心坐標系
質心坐標系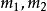 質心坐標系
質心坐標系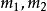 質心坐標系
質心坐標系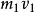 質心坐標系
質心坐標系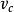 質心坐標系
質心坐標系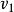 質心坐標系
質心坐標系先求在實驗室系中質心的速度。根據質心的定義得知,質點組的總動量應等於質點組的總質量和質心速度的乘積,由下圖得。由此求出質心相對於實驗室系的速度等於。由於粒子除相互作用外不受外力作用,所以由粒子組成的質點組總動量守恆,亦即在整個碰撞過程中,粒子的總動量永遠等於。因此,在整個碰撞過程中質心速度。的方向永遠平行於入射粒子的入射速度,亦即沿著與x軸平行的方向。
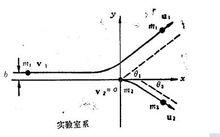 圖2:實驗室系中的斜碰撞
圖2:實驗室系中的斜碰撞根據由伽利略變換得出的速度合成定理,可以求得入射粒子和靶粒子相對於實驗室系與質心繫的入射速度和出射速度之間的關係:
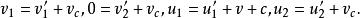 質心坐標系
質心坐標系由圖1和圖2得
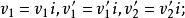 質心坐標系
質心坐標系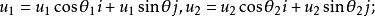 質心坐標系
質心坐標系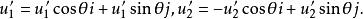 質心坐標系
質心坐標系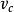 質心坐標系
質心坐標系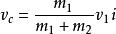 質心坐標系
質心坐標系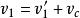 質心坐標系
質心坐標系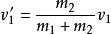 質心坐標系
質心坐標系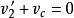 質心坐標系
質心坐標系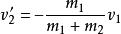 質心坐標系
質心坐標系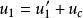 質心坐標系
質心坐標系而質心相對於實驗室系的速度為。代入速度合成定理,由得。由得,由得
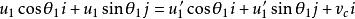 質心坐標系
質心坐標系即
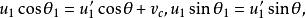 質心坐標系
質心坐標系由
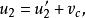 質心坐標系
質心坐標系得
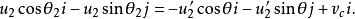 質心坐標系
質心坐標系即
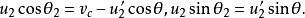 質心坐標系
質心坐標系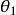 質心坐標系
質心坐標系 質心坐標系
質心坐標系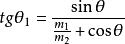 質心坐標系
質心坐標系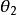 質心坐標系
質心坐標系 質心坐標系
質心坐標系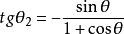 質心坐標系
質心坐標系由此得出入射粒子在實驗室系中的散射角和在質心繫中的散射角之間的關係為,而靶粒子在實驗室系中的散射角和在質心繫中的散射角之間的關係為。
