簡介
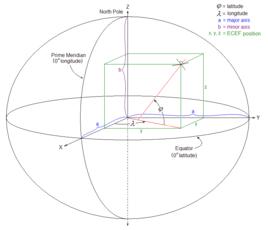
地心地固坐標系（ Earth- Centered, Earth- Fixed，簡稱 ECEF）簡稱 地心坐標系，是一種以地心為原點的地固坐標系（也稱地球坐標系），是一種笛卡兒坐標系。原點 O (0,0,0)為地球質心，z 軸與地軸平行指向北極點，x 軸指向本初子午線與赤道的交點，y 軸垂直於xOz平面(即東經90度與赤道的交點)構成右手坐標系。
笛卡爾坐標系
在數學裡， 笛卡爾坐標系（英語：Cartesian coordinate system），也稱 直角坐標系，是一種正交坐標系。參閱圖1，二維的直角坐標系是由兩條相互垂直、相交於原點的數線構成的。在平面內，任何一點的坐標是根據數軸上對應的點的坐標設定的。在平面內，任何一點與坐標的對應關係，類似於數軸上點與坐標的對應關係。
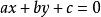地心地固坐標系
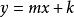地心地固坐標系
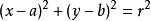地心地固坐標系採用直角坐標，幾何形狀可以用代數公式明確的表達出來。幾何形狀的每一個點的直角坐標必須遵守這代數公式。例如：直線可以標準式、斜截式等式子來表示;一個圓，半徑為r，圓心位於(a,b)。圓圈可以用以表示。
取向
二維空間
直角坐標系的x-軸與y-軸必須相互垂直。稱包含y-軸的直線為y-線。在二維空間裡，當我們設定了x-軸的位置與方向的同時，我們也設定了y-線的方向。可是，我們仍舊必須選擇，在y-線的以原點為共同點的兩條半線中，那一條半線的點的坐標是正值的，那一條是負值的？任何一種選擇決定了xy-平面的取向。
參閱圖1。通常，我們選擇的取向是，正值的x-軸橫地指向右方，正值的y-軸縱地指向上方。這種取向稱為 正值取向， 標準取向，或 右手取向。
右手定則是一種常用的記憶方法，專門用來辨認正值取向：將一隻半握拳的右手放在平面上，大拇指往上指，那么，其它的手指都從x-軸指向y-軸。
另外一種取向，採用 左手定則，專門用來辨認 負值取向，或 左手取向：將一隻半握拳的左手放在xy-平面上，大拇指往上指，那么，其它的手指都從y-軸指向x-軸。
不論坐標軸是何種取向，將坐標系統做任何角度的旋轉，取向仍舊會保持不變。
三維空間
直角坐標系的x-軸，y-軸，與z-軸必須相互垂直。稱包含z-軸的直線為z-線。在三維空間裡，當我們設定了x-軸，y-軸的位置與方向的同時，我們也設定了z-線的方向。可是，我們仍舊必須選擇，在z-線以原點為共同點的兩條半線中，哪一條半線的點的坐標是正值的，哪一條是負值的？這兩種不同的坐標系統，稱為 右手坐標系與 左手坐標系。右手坐標系又稱為 標準坐標系，或 正值坐標系。
右手坐標系這名詞是由右手定則而來的。先將右手的手掌與手指伸直。然後，將中指指嚮往手掌的掌面半空間，與食指呈直角關係。再將大拇指往上指去，與中指，食指都呈直角關係。則大拇指，食指，與中指分別表示了右手坐標系的x-軸，y-軸，與z-軸。同樣地，用左手也可以表示出左手坐標系。
圖8試著展示出一個左手坐標系與一個右手坐標系。因為我們用二維畫面來展示三維物體，會造成扭曲或模稜兩可的圖形。指向下方與右方的軸，也有指向讀者的意思；而位置居於中間的軸，也有指向讀者正在看的方向的意思。平行於xy-平面的紅色圓形曲箭，其紅色箭頭從z-軸前面經過，表示從x-軸往y-軸的旋轉方向。
參閱
•廣義坐標
•正則坐標
•平行坐標
•象限角
•卦限
•正交坐標系
