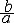multinomialinequality
有理不等式中的一類。兩個整式由不等號連結而成的不
等式。這兩個整式次數的較大者定義為不等式的次數。如2x＋3＞0為一次不等式，x2＋3x＞2，x2＋y2≥2xy為二次不等式。
在解不等式問題中，最基本的整式不等式有：
①一元一次不等式。兩邊都是一元一次整式的不等式，通過同解變形，化為標準形式ax＋b＞0，x表未知數，若a≠0，則a＞0時，解得－
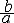＜x＜＋∞；a＜0時，解得－∞＜x＜－
。若a＝0，則b＞0時，解是所有實數；b＜0時無解。②一元二次不等式。兩邊都是一元二次整式的不等式，同解變形化為標準形式ax2＋bx＋c＞0。若a＞0，取判別式Δ＝b2－4ac，則當Δ＞0時，解得x＜
或x＞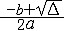
；當Δ＝0時，x為除-2
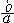外所有實數，當△＜0時，解得
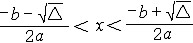；當△≤0時，無解。若a=0，不等式bx＋c＞0同解，按一元一次不等式處理。③二元一次不等式。有代表性的一種形式是ax＋by＋c＞0，a，b，不全為零，x，y，為未知數，每個解是一個序偶(x，y)，對應坐標平面上一個點，解集對應直線ax＋by＋c=0一側的半個平面，b＞0時上側，b＜0時為下側。
