收斂數列

設數列Xn，如果存在常數a，對於任意給定的正數q（無論多小），總存在正整數N，使得n>N時，恆有|Xn-a|

性質

唯一性

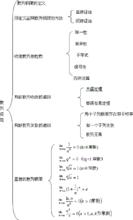思維導圖

如果數列Xn收斂，每個收斂的數列只有一個極限。

有界性

定義：設有數列Xn , 若存在M>0,使得一切自然數n,恆有|Xn|<M成立，則稱數列Xn有界。

定理1：如果數列{Xn}收斂，那么該數列必定有界。推論：無界數列必定發散；數列有界

，不一定收斂；數列發散不一定無界。

數列有界是數列收斂的必要條件，但不是充分條件

保號性

如果數列{Xn}收斂於a，且a>0（或a<0），那么存在正整數N，當n>N時，都有Xn>0（或Xn<0）。

相互關係

收斂數列與其子數列間的關係

子數列也是收斂數列且極限為a恆有|Xn|<M

若已知一個子數列發散，或有兩個子數列收斂於不同的極限值，可斷定原數列是發散的。

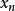收斂數列

如果數列{}收斂於a，那么它的任一子數列也收斂於a。