給定數列{Xn}:X1,X2,…,Xn,…,在這個數列里,任取無窮多項,不改變它們在原來數列中的先後次序,得到的數列稱為是原來數列的一個子數列,任何一個數列都存在無窮多個子數列。如果原來數列極限存在,則得到的子數列極限存在。
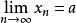 收斂子數列
收斂子數列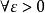 收斂子數列
收斂子數列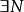 收斂子數列
收斂子數列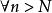 收斂子數列
收斂子數列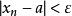 收斂子數列
收斂子數列證明:由, 可知,, s.t.,
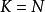 收斂子數列
收斂子數列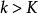 收斂子數列
收斂子數列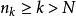 收斂子數列
收斂子數列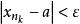 收斂子數列
收斂子數列令, 當時,, 成立

收斂子數列是一個數列,在這個數列里,任取無窮多項,不改變它們在原來數列中的先後次序,得到的數列稱為是原來數列的一個子數列,任何一個數列都存在無窮多個子數列。
給定數列{Xn}:X1,X2,…,Xn,…,在這個數列里,任取無窮多項,不改變它們在原來數列中的先後次序,得到的數列稱為是原來數列的一個子數列,任何一個數列都存在無窮多個子數列。如果原來數列極限存在,則得到的子數列極限存在。
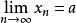 收斂子數列
收斂子數列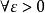 收斂子數列
收斂子數列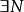 收斂子數列
收斂子數列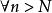 收斂子數列
收斂子數列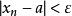 收斂子數列
收斂子數列證明:由, 可知,, s.t.,
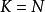 收斂子數列
收斂子數列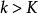 收斂子數列
收斂子數列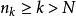 收斂子數列
收斂子數列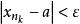 收斂子數列
收斂子數列令, 當時,, 成立
設數列XnN時,恆有|Xn-a|
性質 保號性 相互關係數列的極限問題是我們學習的一個比較重要的部分,同時,極限的理論也是高等數學的基礎之一。數列極限的問題作為微積分的基礎概念,其建立與產生對微積分的理論有著...
基本概念 性質 存在的條件 套用收斂級數(convergent series)是柯西於1821年引進的,它是指部分和序列的極限存在的級數。收斂級數分條件收斂級數和絕對收斂級數兩大類,其...
預備知識 定義 基本性質 級數收斂性給定數列Xn,從中任意地選取無限項,按照原來的順序組成的數列稱為數列Xn的一個子列。 子列是數列與它的任一平凡子列同為收斂或發散,且在收斂時有相同的極限。
定義 子列定理造出兩個具有不同收斂極限的子數列,就可以說明這個數列是發散的。(2)如果...{的子數列{和{都收斂於同一個極限,那么數列{也收斂於這個極限。顯然這個...的子數列。(5)如果一個數列是由兩個收斂數列通過四則運算得到的,那么這個...
數列的極限。 函式的極限數列,或者是構造出兩個具有不同收斂極限的子數列,就可以說明這個數列是發散...數列的極限。並且稱數列收斂於極限a。我們使用記號來表示這點。否則我們就說數列{an}是發散的。 這就是一個數列收斂於一個極限或者說存在一個...
數列的極限。 函式的極限的有界性;③收斂數列的子列性質。 ...的稱為不定向發散序列。例如,數列{q},當|q| 1及q=1時,分別收斂...於一點,向某一值靠近。收斂類型有收斂數列、函式收斂、全局收斂、局部收斂...
概念 序列 收斂 發散 發散數列。 無窮級數 無窮級數 無窮級數 無窮級數 5 、收斂級數的部分和數列的子數列...的:正項級數收斂的充要條件是部分和數列有界。有界性可以通過許多途徑來進行...,理論以數項級數為基礎,數項級數有發散性和收斂性的區別。無窮級數收斂時有...
概述 歷史 記號 性質 冪級數使之收斂到極限0,就說這個變數成為無窮小。”柯西把無窮小視為“以0為極限...
極限思想 數列極限 函式極限