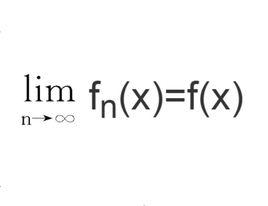函式列

函式列(sequence of functions)指各項為具有相同定義域的函式的序列。若fn為函式列，其中每個函式fn的定義域為A，則A也稱為fn的定義域，若對某個x0∈A，數列fn(x0)收斂，則x0稱為fn的收斂點，或稱fn在點x0收斂，fn的所有收斂點的集合稱為它的收斂域。若對每個x∈D，有當n→∞時，fn(x)→f(x)，則函式f(x)稱為函式列fn(或fn(x))在D上的極限函式，這時也說，函式列fn在D上處處收斂於f，或在D上逐點收斂於f。對一般的函式列來說，除研究它的逐點收斂(或稱點態收斂)這種收斂方式外，還要研究一致收斂，這是為了研究極限函式是否繼承相應函式列的各項(函式)所具有的分析性質(連續、可微、可積等)而引入的一種收斂方式 。

基本概念

設

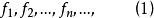函式列

是一列定義在同一數集E上的函式，稱為定義在E上的函式列 。也可簡記為

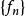函式列

或

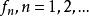函式列

函式列的收斂性

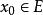函式列

設 ，將x代人函式列(1)得到數列：

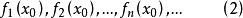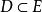函式列

函式列

若數列(2)收斂，則稱函式列(1)在點x收斂，x稱為函式列(1)的收斂點。若數列(2)發散，則稱函式列(1)在點x發散，若函式列(1)在數集 上每一點都收斂，則稱函式列（1）在數集D上收斂，函式列{f}全體收斂點的集合，稱為函式列{f}的收斂域 。

函式列的極限函式

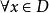函式列

函式列

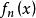函式列

若函式列(1)在數集D上收斂，這時 ，都有數列{ }的一個極限值與之對應，由這個對應法則就確定了D上的一個函式，稱它為函式列{f}的極限函式，記作 ，於是有

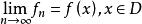函式列

或

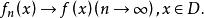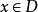函式列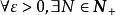

函式列

函式列

函式列極限的ε-N定義：對每一個固定的 ，對 （注意：一般說來N值的確定與ε和x的值都有關），使得當n>N時，總有

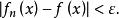函式列

函式列的一致收斂性

函式列一致收斂性的定義

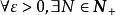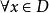函式列

函式列

設{f}與f定義在數集D上，若 ，當n>N時， ，都有

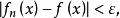函式列

則稱函式列{f}在D上一致收斂於f，記作

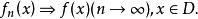函式列

函式列一致收斂性的判別

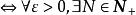函式列

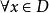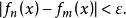函式列

函式列

(1) 柯西準則：{f}在D上一致收斂 ，當n，m>N時， ，都有

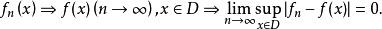函式列

(2) 餘項準則：