清一色
 數字
數字 12345679×9=111111111
12345679×18=222222222
12345679×27=333333333
12345679×36=444444444
12345679×45=555555555
12345679×54=666666666
12345679×63=777777777
12345679×72=888888888
12345679×81=999999999
三位一體
“缺8數”引起研究者的濃厚興趣,於是人們繼續拿3的倍數與它相乘,發現乘積竟“三位一體”地重複出現。例如:
12345679×12=148148148
12345679×15=185185185
12345679×57=703703703
輪流休息
當乘數不是3的倍數時,此時雖然沒有“清一色”或“三位一體”現象,但仍可看到一種奇異性質:乘積的各位數字均無雷同。缺什麼數存在著明確的規律,它們是按照“均勻分布”出現的。另外,在乘積中缺3、缺6、缺9的情況肯定不存在。
讓我們看一下乘數在區間【10—17】的情況,其中12和15因是3的倍數,予以排除。
12345679×10=123456790(缺8)
12345679×11=135802469(缺7)
12345679×13=160493827(缺5)
12345679×14=172839506(缺4)
12345679×16=197530864(缺2)
12345679×17=209876543(缺1)
乘數在【19—26】及其他區間(區間長度等於7)的情況與此完全類似。
乘積中缺什麼數,就像工廠或商店中職工“輪休”,人人有份,但也不能多吃多占,真是太有趣了!
一以貫之
當乘數超過81時,乘積將至少是十位數,但上述的各種現象依然存在,真是“吾道一以貫之”。隨便看幾個例子:
(1)乘數為9的倍數
12345679×243=2999999997,只要把乘積中最左邊的一個數2加到最右邊的7上,仍呈現“清一色”。
(2)乘數為3的倍數,但不是9的倍數
12345679×84=1037037036,只要把乘積中最左邊的一個數1加到最右邊的6上,又可看到“三位一體”現象。
(3)乘數為3K+1或3K+2型
12345679×98=1209876542,表面上看來,乘積中出現雷同的2,但據上所說,只要把乘積中最左邊的數1加到最右邊的2上去之後,所得數為209876543,是“缺1”數,而根據上面的“學說”可知,此時正好輪到1休息,結果與理論完全吻合。
走馬燈
冬去春來,24個節氣仍然是立春、雨水、驚蟄……其次序完全不變,表現為周期性的重複。“缺8數”也有此種性質,但其乘數是相當奇異的。
實際上,當乘數為19時,其乘積將是234567901,像走馬燈一樣,原先居第二位的數2卻成了開路先鋒。深入的研究顯示,當乘數為一公差等於9的算術級數時,出現“走馬燈”現象。例如:
12345679×28=345679012
12345679×37=456790123
回文結對
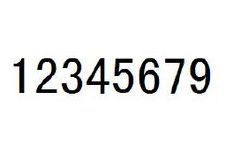 缺八數
缺八數 12345679×4=49382716
12345679×5=61728395
前一式的積數顛倒過來讀(自右到左),不正好就是後一式的積數?(但有微小的差異,即5代以4,而根據“輪休學說”,這正是題中的應有之義。)
這樣的“回文結對,攜手並進”現象,對13,14;22,23;31,32;40,41等各對乘數(每相鄰兩對乘數的對應公差均等於9)也應如此。例如:
12345679×67=827160493
12345679×68=839506172
遺傳因子
“缺8數”還能“生兒育女”,這些後裔秉承其“遺傳因子”,完全承襲上面的這些特性,所以這個龐大家族的成員幾乎都同其始祖12345679具有同樣的本領。
例如50672839是“缺8數”與41的乘積,所以它是一個衍生物。
我們看到,506172839×3=1518518517。
如前所述,“三位一體”模式又來到我們面前。
追本窮源
“缺8數”實際上與循環小數是一根藤上的瓜,因為
1/81=0.012345679。
在0.012345679中,為什麼別的數碼都不缺,應有盡有,而唯獨缺少8呢?
我們看到,1/81=1/9×1/9。
把1/9化成循環小數,其循環節只有一位,即1/9=0.1。
如果你不怕麻煩,當然也可把它看成是0.1111……直到無窮。
無窮多個1的自乘,能辦得到嗎?不妨先從有限個1的平方來試試看。
很明顯:11的平方=121,111的平方=12321,……,直到111111111的平方=12345678987654321。
但現在是無窮個1相乘,長長的隊伍看不到盡頭,怎么辦呢?
利用數學歸納法,不難證明,在所有的層次,8都被一一跳過。
循環小數與循環群、周期現象的研究正方興未艾,它已引起許多人的濃厚興趣與密切關注。由於計算機科學的蓬勃發展,人們越來越不滿足於泛泛的幾條性質,而更著眼於探索其精微結構。
其他類型
也許有人以為缺八數是10進制下的特有情況,但事實是,16進制下也有類似的數字出現。
10進制中缺8數關於乘數3的性質是由關於乘數9的性質衍生而來的,在8進制中沒有類似的性質。
16進制中缺8數為:123456789abcdf
123456789abcdf×f=111111111111111
如前所述,缺8數的出現與循環小數有密切的聯繫。
在任何一種進制中,1除以最大的個位數,得到的都是0.1111...無限循環的小數,缺8數的全部性質理論上應該都能由此推出。
可以認為,缺8數的性質是由進制的規則決定的,是進制性質的反應。

