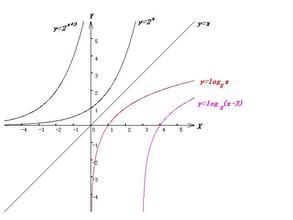
基本簡介
一般形式
不給出具體解析式,只給出函式的特殊條件或特徵的函式即抽象函式。一般形式為y=f(x),或許還附有定義域、值域等,如:y=f(x),(x>0,y>0)。其它形式
冪函式:f(xy)=f(x)f(y)正比例函式:f(x+y)=f(x)+f(y)
對數函式:f(x)+f(y)=f(xy)
三角函式:f(x+y)+f(x-y)=2f(x)f(y)f(x)=cosx
指數函式:f(x+y)=f(x)f(y)
周期為n的周期函式:f(x)=f(x+n)
證明
 抽象函式定義域
抽象函式定義域證明:定義域:相同
∵f(2*1)=f(2)+f(1)∴f(1)=0
∵f(1)=f(2)+f(1/2)∴f(1/2)=-1同理f(1/x)=-f(x)
∵f(x^k)=f(x*x*……*x*x)【k個x】=f(x)+f(x)+……+f(x)+f(x)【k個】=k*f(x),k∈Z且k>0(x=2時f(x^k)=k)①
f(x^k)=f((1/x)^(-k))=f((1/x)*(1/x)*……*(1/x)*(1/x))【-k個x】=f(1/x)+f(1/x)+……+f(1/x)+f(1/x)【-k個】=(-k)*f(1/x),k∈Z且k<0(x=2時,f(x^k)=-k*f(1/2)=k)
f(x^0)=f(1)=0=0*f(x)(x=2時,f(x^k)=k=0)
∴f(2^k)=k,k∈Z②
∵p*f(2^(1/p))=f((2^(1/p))^p)=f(2^(1/p*p))=f(2)=1,k<>0且p∈Z(①)
∴f(2^(1/p))=1/p,p∈Z且p<>0
又∵②∴f(2^(k/p))=f((2^(1/p))^k)=k*f(2^(1/p))=k*(1/p)*f(2)=k/p即f(2^m)=m對所有有理數成立③
任取z∈R,{1}若f(2^z)<z,z必定為f(y),y>2^z(由於單調性以及③),
在(2^z,y)上必定有q=2^(z+n),z+n為有理數,n>0,
f(q)=z-n<f(y)=z(單調性)與n>0矛盾,導出矛盾所以f(2^z)<z不成立
{2}同理f(2^z)>z不成立
又∵2^z>0,有定義域
所以f(2^z)=z
令x=2^z>0,f(x)=z=以二為底2^z的對數=以二為底x的對數
證畢。(若沒有單調性要先證單調性)
表達形式
f(m+x)=f(n-x)對稱軸為(m+n)/2f(m+x)+f(n-x)=1關於((m+n)/2,1/2)對稱
f(x+m)=f(x)周期為m
微分方程
求解抽象函式 微分方程
微分方程學好函式
熟悉函式的基本知識解答抽象函式題目的基礎是熟悉函式的基本知識。如果連基本的函式知識都沒有掌握,解決抽象函式問題只能是空談。具體說,學好函式要掌握常見函式的性質。例如,中學涉及的函式性質一般有單調性、奇偶性、有界性及周期性;常見的函式有指數函式、對數函式、三角函式、二次函式、對勾函式(Y=X+A/X(A>0))等等。靈活選擇解題方法從上文對幾種解法的介紹不難看出,選擇合適的方法對解決抽象函式問題往往會起到事半功倍的效果。對於選擇題,選用特殊值法、賦值法、圖像法等等可以在很短的時間內得到答案,在應試時節省出不少時間。而對各種方法的理解,在解題中選擇出合適的方法,則需要在平時的學習中多體會多感悟。
解法舉例
特殊值法
 抽象函式定義域
抽象函式定義域例1定義在R上的函式f(x)滿足f(x+y)=f(x)+f(y)(x,y∈R),當x<0時,f(x)>0,則函式f(x)在[a,b]上()
A 有最小值f(a)B有最大值f[(a+b)/2] C有最小值f(b)D有最大值f(b)
分析:許多抽象函式是由特殊函式抽象背景而得到的,如正比例函式f(x)=kx(k≠0),可抽象為f(x+y)=f(x)+f(y),與此類似的還有
特殊函式
抽象函式
f(x)=x
f(xy)=f(x)f(y)
f(x)=0
f(x+y)=f(xy)
f(x)=logax
f(xy)=f(x)+f(y)
此題作為選擇題可採用特殊值函式f(x)=kx(k≠0)
∵當x<0時f(x)>0即kx>0。.∴k<0,可得f(x)在[a,b]上單調遞減,從而在[a,b]上有最小值f(b)。
賦值法
根據所要證明的或求解的問題使自變數取某些特殊值,從而解決問題。例2除了用剛才的方法外,也可採用賦值法
解:令y=-x,則由f(x+y)=f(x)+f(y)(x,y∈R)得f(0)=f(x)+f(-x)…..①,
再令x=y=0得f(0)=f(0)+f(0)得f(0)=0,代入①式得f(-x)=-f(x)。
得f(x)是一個奇函式,圖像關於原點對稱。
∵當x小於0時,f(x)>0,
即f(x)在R上是一個減函式,可得f(x)在[a,b]上有最小值f(b)。
圖像性質解法
抽象函式雖然沒有給出具體的解析式,但可利用它的性質圖象直接來解題。抽象函式解題時常要用到以下結論:
定理1:如果函式y=f(x)滿足f(a+x)=f(b-x),則函式y=f(x)的圖象關於x=(a+b)/2對稱。
定理2:如果函式y=f(x)滿足f(a+x)=f(b+x),則函式y=f(x)是一個周期函式,其周期應為∣b-a∣
例4 f(x)是定義在R上的偶函式,且f(x)=f(2-x),證明f(x)是周期函式。
分析:由f(x)=f(2-x),得f(x)的圖象關於x=1對稱,又f(x)是定義在R上的偶函式,圖象關於y軸對稱,根據上述條件,可先畫出符合條件的一個圖,那么就可以化無形為有形,化抽象為具體。從圖上直觀地判斷,然後再作證明。
由圖可直觀得T=2,要證其為周期函式,只需證f(x)=f(2+x)。
證明:f(x)=f(-x)=f[2-(-x)]=f(2+x),∴T=2。
∴f(x)是一個周期函式。
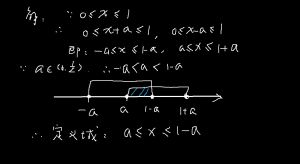
例5已知定義在[-2,2]上的偶函式f(x)在區間[0,2]上單調遞減,若f(1-m)<f(m),求實數m的取值範圍
分析:根據函式的定義域,-m,m∈[-2,2],但是1-m和m分別在[-2,0]和[0,2]的哪個區間內呢?如果就此討論,將十分複雜,如果注意到偶函式,則f(x)有性質f(-x)=f(x)=f(|x|),就可避免複雜的討論。