概念引入
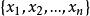 線性獨立
線性獨立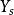 線性獨立
線性獨立例如,一個運輸企業Y有n輛汽車,那么Y(在單位時間)的收入(記為)可表為
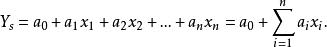 線性獨立
線性獨立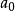 線性獨立
線性獨立這是個線性函式,其係數表示各自的貢獻率,可以為0或負數,比如可表企業的定常支出等。這時則說(企業內)各車之間的關係是線性的。
特別地,所謂“線性關係”的本質就是“獨立關係”(又叫線性獨立),因為這時任何一輛車的“貢獻”大小和有無(即其係數取正負、大小及是否取0等)皆與別的車無關。
定義
若有m+1個n維不全為零的向量
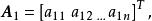 線性獨立
線性獨立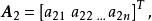 線性獨立
線性獨立 線性獨立
線性獨立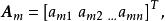 線性獨立
線性獨立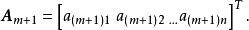 線性獨立
線性獨立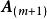 線性獨立
線性獨立如果其中第個向量可以寫成
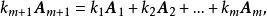 線性獨立
線性獨立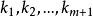 線性獨立
線性獨立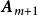 線性獨立
線性獨立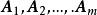 線性獨立
線性獨立這裡為常數,則稱這m+1個向量之間存在著線性關係;又稱這m+1個向量線性相關;或稱是的線性表出。當然,由上式可知若這m+1個向量是線性相關的,必可寫成
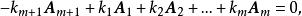 線性獨立
線性獨立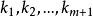 線性獨立
線性獨立這裡必不全為零。
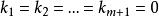 線性獨立
線性獨立顯然,若這m+1個向量不能夠寫成上面兩個式子的形式,或者換個說法只有當的情況下以上兩式才成立,則稱這m+1個向量是 線性獨立的。
舉例說明
例如有以下三個向量
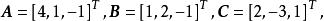 線性獨立
線性獨立它們是線性相關的,因為 A可以由 B、 C線性表出,即 A=2 B+ C。
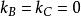 線性獨立
線性獨立若將 A向量除去,向量 B與向量 C則是線性獨立的,這是因為 B≠k C,k為任意常數.或者說只有才能使得
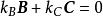 線性獨立
線性獨立成立,所以 B與 C是線性獨立的。
關係
線性獨立與矩陣秩的關係
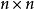 線性獨立
線性獨立不難證明若有階矩陣
 線性獨立
線性獨立如果它的n個行(列)向量是線性獨立的,則該方陣的秩為n,反之如果其n個行向量或n個列向量是線性相關的,則其秩一定小於n,綜上所述,可得定理如下:
定理1
n×n階矩陣秩為n的充分必要條件是n個行向量或n個列向量是線性獨立的。
讓我們以矩陣
 線性獨立
線性獨立為例,對以上定理加以驗證.由於該矩陣的三個行向量是線性相關的,故以-2乘第二行向量,以-1乘第三行向量,然後都加到第一行上去,則得到第一行全為零的矩陣
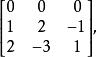 線性獨立
線性獨立故該矩陣的秩小於n,反之,若矩陣的n個行向量或列向量是線性獨立的,則無論怎樣進行初等變換,也不可能將它變成某一行或某一列為零向量的形式,例如矩陣
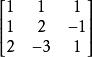 線性獨立
線性獨立就是這樣的,該矩陣滿秩,秩等於3。
定理2
設 A為m×n階矩陣,如果rank A=r,則其m個行向量中有r個是線性獨立的,其他(m—r)個行向量可用其線性組合表出。此外n個列向量中也有r個是線性獨立的,其它(n-r)個列向量亦可用其線性組合表出。
由此可知, A矩陣的秩的數目就是 A矩陣的最大的線性獨立的行(列)向量的數目。例如
 線性獨立
線性獨立因為該矩陣的位於左上角的二階子行列式
 線性獨立
線性獨立而所有3階子行列式皆等於零,故
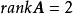 線性獨立
線性獨立則其第一列和第二列是線性獨立的,第三列,第四列可以用第一列與第二列線性組合來表示,即
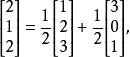 線性獨立
線性獨立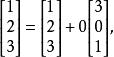 線性獨立
線性獨立由定理2直接可推斷出以下定理。
定理3
設 A為m×n階矩陣,又已知m≤n,如果其中m個行向量是線性獨立的,則 A矩陣有最大可能的秩,其秩為m。如果n≤m,若其中n個列向量是線性獨立的,則 A矩陣有最大可能的秩,其秩為n。
如果 A矩陣具有最大可能的秩,即rank A=min(m,n),則稱 A矩陣為最大秩矩。