暫態時域分析
正文
電路在暫態中的行為由其中的電流、電壓等變數來描述。而這些變數滿足電路的方程。集總參數電路可由一組常微分方程描述。對一電路,由其結構決定的 KCL、KVL方程(拓撲約束,見基爾霍夫定律)和各電路的元件方程(元件約束)可導出該電路的方程。對於線性電路,這樣的方程是線性微分方程。所有電路元件都是恆定值的線性電路稱為線性時不變電路,其方程是常係數線性微分方程;而含有線性時變元件的電路稱為線性時變電路,其方程是線性變係數微分方程。線性時不變電路是常見的,與線性時不變電路有關的分析研究方法和技術都較為成熟。線性時不變電路的暫態分析常用時域分析方法和頻域分析方法,後者還包括復頻域分析。暫態的時域分析是直接利用微分方程的求解方法求解;後者是對電路變數的方程加以變換,如作拉普拉斯變換、傅立葉變換,然後求解。較大規模的電路的暫態分析還可用數字計算機求數值解,或進行模擬實驗研究。
電路的暫態分析在電工技術中有著重要的意義。電力系統本身就是含有多種元件的電路,在各種激勵、擾動、操作下,電路中的暫態行為與其設計、運行都有著密切的關係。對在暫態中可能出現的過電壓、過電流必須有預防或保護措施,以免造成危害;在多種的自動控制系統中,電路往往是系統中的環節,其暫態行為常直接關係到系統工作情況的品質。所以電路的暫態分析與控制系統的分析是緊密相關的。這使得電路的暫態分析成為與多方面的技術有密切關係的電工理論的重要部分。
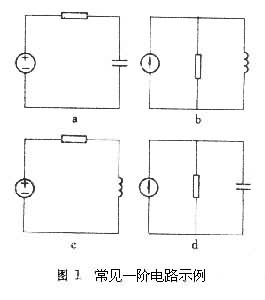
一階電路 可用一階常微分方程描述的電路。通常是指以線性一階常係數微分方程描述的電路。從電路特徵看,僅含一個貯能元件(常值電容與電感)和電阻的電路,或能化為此形式的電路,都可用這樣的方程描述,都屬於一階電路。圖1中示有4個常見的一階電路,其中b、d分別是a、c的對偶電路。
 暫態時域分析
暫態時域分析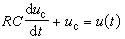
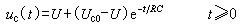
 圖2a、2b是此電路中uc(t)的曲線。電路中的電流i是
圖2a、2b是此電路中uc(t)的曲線。電路中的電流i是 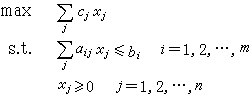 t>0
t>0
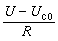 依指數規律衰減。圖2c、2d是表示電流變化的曲線。
依指數規律衰減。圖2c、2d是表示電流變化的曲線。 一階電路動態過程中都有一項由Ae
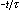 表示的暫態分量,其中的τ是由電路微分方程的特徵方程求得。例如(1)式的特徵方程是RCS +1=0,便有
表示的暫態分量,其中的τ是由電路微分方程的特徵方程求得。例如(1)式的特徵方程是RCS +1=0,便有 ,τ=RC。τ具有時間的量綱,稱為時間常數。圖1a、1d中的電路的時間常數是RC,圖1b、1c中的電路的時間常數是L/R。
,τ=RC。τ具有時間的量綱,稱為時間常數。圖1a、1d中的電路的時間常數是RC,圖1b、1c中的電路的時間常數是L/R。 由時間常數的大小容易判斷一階電路中暫態分量衰減的快慢,每經過時間間隔T,暫態分量衰減至此時間間隔起始值的
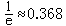 。從動態過程開始。經過(4~5)T的時間,暫態分量衰減到其初始值的(0.018~0.00673),便可認為暫態分量實際上已消失。在電路激勵為恆定值的情況下,經過這一時間,便可認為電路達到了它的恆定的穩態。
。從動態過程開始。經過(4~5)T的時間,暫態分量衰減到其初始值的(0.018~0.00673),便可認為暫態分量實際上已消失。在電路激勵為恆定值的情況下,經過這一時間,便可認為電路達到了它的恆定的穩態。 若圖1a的電路中的激勵為一正弦電壓,u=Umsinωt,則電容電壓uc的穩態亦為同頻正弦量,其暫態過程如圖3所示。
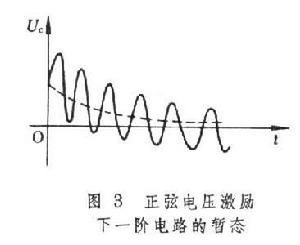 暫態時域分析
暫態時域分析二階電路 可以用二階常微分方程描述的電路。通常是指以線性二階常係數微分方程描述的電路。從電路特徵上看,含有2個貯能元件(電感、電容)和若干電阻,但不含電容與電壓源迴路或電感與電流源割集的電路,以及能化為此形式的電路,都屬於二階電路。
 暫態時域分析
暫態時域分析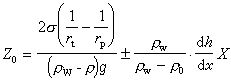 (1)
(1)
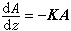 (2)
(2)
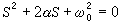
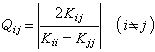
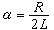 (阻尼或衰減係數),
(阻尼或衰減係數),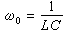 (諧振角頻率)。在電感和電容上的起始條件iL)(0)=0和uc(0)=0的情況下,可得
(諧振角頻率)。在電感和電容上的起始條件iL)(0)=0和uc(0)=0的情況下,可得 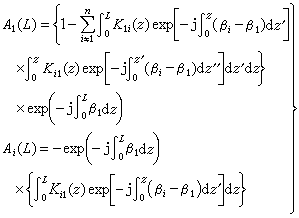
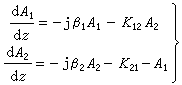
①
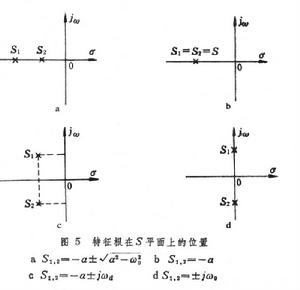
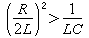 ,S1,2是兩個相異的負實根,這種情況稱過阻尼過程。這時阻尼作用強,過程不會出現振盪。阻尼係數α 越大,進入穩態所需的時間越長。
,S1,2是兩個相異的負實根,這種情況稱過阻尼過程。這時阻尼作用強,過程不會出現振盪。阻尼係數α 越大,進入穩態所需的時間越長。 ②
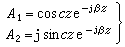 ,S1,2是兩個相等的負實根,這種情況稱臨界阻尼過程。
,S1,2是兩個相等的負實根,這種情況稱臨界阻尼過程。 ③
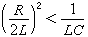 ,S1,2是一對共軛復根,這種情況稱欠阻尼過程。在這一情況下,暫態過程中出現衰減振盪,振盪的振幅逐漸減小,最終衰減到零,電路就進入穩態。
,S1,2是一對共軛復根,這種情況稱欠阻尼過程。在這一情況下,暫態過程中出現衰減振盪,振盪的振幅逐漸減小,最終衰減到零,電路就進入穩態。 ④R=0,α=0,S1,2是共軛虛根,這種情況稱等幅振盪過程。這時無阻尼作用,電感中的磁能和電容中的電能不斷交換,形成振幅一定的振盪。
 暫態時域分析
暫態時域分析高階電路 描述線性時不變的動態電路中的n 階常微分方程
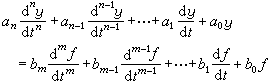
電路的階數與電路的複雜度有關。對一個正則的RLC元件電路,電路階數n等於貯能元件個數。若存在純電容或電容與電壓源形成的迴路,或存在純電感或電感與電流源形成的割集,階數將減少。一般情況下,電路階數都不會高於它的貯能元件數。
常係數線性微分方程解的特徵主要取決於它的特徵方程。方程(3)的特徵方程為
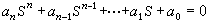
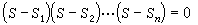
根據系統理論,任意輸入為f(t)的n階電路的全回響,在特徵方程無重根的情況下可以下式表示
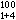
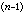 (0)n 個起始條件在輸入為零的條件下確定;右端積分項為用電路的衝激回響h(t)與輸入f(t)的卷積公式表達的零狀態回響。
(0)n 個起始條件在輸入為零的條件下確定;右端積分項為用電路的衝激回響h(t)與輸入f(t)的卷積公式表達的零狀態回響。