簡介
雙曲守恆律方程組
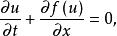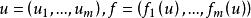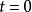黎曼問題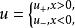
黎曼問題
黎曼問題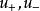
黎曼問題
黎曼問題其中，的一類初值問題，其初值為,，其中，為不同的 m 維常向量。
黎曼問題由黎曼（G.F.B.Riemann）所提出。一般的黎曼問題則是美國著名數學家拉克斯（D.D.Lax）首先開始研究的，在方程為嚴格雙曲以及方程的所有特徵或為真正非線性，或為線性退化的假設下，拉克斯構造了黎曼問題的解，它由 m 個波組成，或為激波或為中心疏散波，或為接觸間斷。黎曼問題在守恆律方程組的理論研究中起著非常基本的作用。計算雙曲守恆律方程組中弱解的許多數值格式，如格利姆格式，都以黎曼問題的解為基礎，此外，雙曲守恆律方程組的整體弱解當時間趨於無窮時，往往趨於一個黎曼問題的解。
相關背景
描寫氣體運動的基本方程是歐拉方程，它由質量、動量和能量三個守恆律組成，它的最大特點和困難在於解中會出現間斷現象，衝擊波就是一種壓縮性的間斷。1858年，黎曼緊緊抓住了間斷現象這一特點，提出並解決了歐拉方程一種最簡單的間斷初值問題即初值為含有一個任意間斷的階梯函式，被後人稱為黎曼問題。
黎曼構造出了它的四類解，它們分別由前、後向疏散波和前、後向衝擊波組裝而成。並利用相平面分析方法給出了此四類解的判別條件。
套用
黎曼問題最初在空氣動力學領域提出，現在是處理帶有間斷流動（如激波）常常要遇到的問題，是計算流體力學領域的基礎性問題之一。
黎曼的這一工作開創了“微分方程廣義解”概念及“相平面分析”方法之先河，具有極大的超前性。黎曼以其敏銳的洞察力和巨大的創造力為非線性雙曲型守恆律的數學理論奠定了第一塊基石。
在計算流體力學中，傳統上，針對可壓縮Navier-Stokes方程的無粘部分和粘性部分分別構造數值方法。其中最為困難和複雜的是無粘部分的離散方法；而粘性項的離散相對簡單，一般採用中心差分離散。所以學者們重點研究的是無粘的歐拉方程的解法。在推廣到Navier-Stokes方程時，只需在歐拉方程的基礎上加上粘性項的離散即可。歐拉方程是一種典型的非線性守恆系統。
