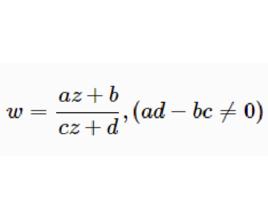基本介紹
由分式線性函式
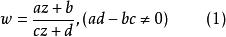分式線性變換所給出的映射叫做 分式線性變換，它有幾個特殊形式：
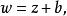分式線性變換（1）平移變換這是整個平面的一個平移，每一個點都移動一個向量b。
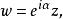分式線性變換
分式線性變換 分式線性變換（2）旋轉變換（是實數），這是以原點為中心的一個旋轉，旋轉角為。
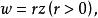分式線性變換（3）相似變換這是一個以原點為中心，伸張係數為r的相似變換。
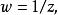分式線性變換
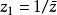分式線性變換
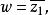分式線性變換（4）倒數變換它又可以分解為:及前者是一個關於單位圓周的反演變換，後者是一個關於實軸的反射變換。
對任意分式線性變換，可分為兩種情況;
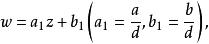分式線性變換1.若c=0，它是一個整線性變換可由（1）一（3）三種簡單變換疊合而成。
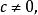分式線性變換
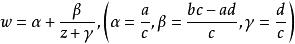分式線性變換2.若把它改寫成，可由（1）—（4）四種簡單變換疊合而成 。
分式線性變換的性質
定理1
任一個分式線性函式(1)，給出一個從閉z平面到閉w平面的雙方單值的保角變換(這裡我們定義兩條曲線交在無窮遠處的角，等於它們在倒數變換下的象曲線在原點的交角) 。
定理2
(保圓性)分式線性變換把圓周變成圓周。
這裡及下面幾個定理中，所說到的圓周，都包括直線在內，也就是說，把直線看成是通過無窮遠點的圓周。這樣，一個圓周經過分式線性變換後，究竟是變成直線還是普通圓周，只要看它上面有沒有無窮遠點就可以確定。
定理3
(保對稱點不變性)分式線性變換把對某一圓周為對稱的點，變為對這個圓周的象對稱的點。
定理4
分式線性變換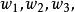
分式線性變換 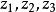分式線性變換 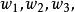分式線性變換任給z平面上三個不同的點和w平面上的三個點則存在唯一個分式線性變換，把分別變為而且這個分式線性變換可表為
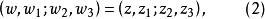分式線性變換
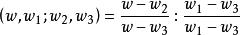分式線性變換這裡。
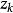分式線性變換
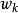分式線性變換
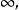分式線性變換
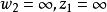分式線性變換如果或中的某一個是只需在(2)式中把含有這個數的因子改為1即可，例如，當時，(2)式成為
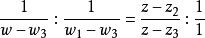分式線性變換即
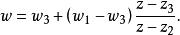分式線性變換 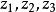分式線性變換
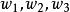分式線性變換
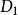分式線性變換
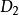分式線性變換
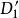分式線性變換
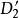分式線性變換
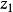分式線性變換
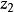分式線性變換
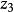分式線性變換
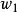分式線性變換
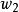分式線性變換
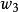分式線性變換由保圓性可知，分式線性變換(1)，把由三點所確定的圓周C，變成由三點所確定的圓周C'，圓周C和C' 分別將z平免和w平面分成兩個區域及和及，而且變換(1)把由經走向時，位在左邊的區域，變成在w平面上，由經走向時，位在左邊的區域。
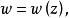分式線性變換
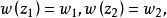分式線性變換利用分式線性變換解題時，下述事實是經常有用的: 如果一個分式線性變換滿足條件則這個變換可以表為
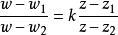分式線性變換(k為任意復常數).
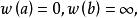分式線性變換
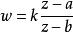分式線性變換特別地，若則。
