概述
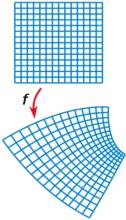 圖1.直角格線和它在共形映射f下的像
圖1.直角格線和它在共形映射f下的像 共形映射
共形映射 共形映射
共形映射數學上,一個 共形變換(保角變換)是一個保持角度不變的映射。更正式的說,一個映射 w=f(z)稱為在 共形(或者 保角),如果它保持穿過的曲線間的定向角度,以及它們的取向也就是說方向。共性變換保持了角度以及無窮小物體的形狀,但是不一定保持它們的尺寸。
共形的性質可以用坐標變換的導數矩陣雅可比矩陣的術語來表述。如果變換的雅可比矩陣處處都是一個標量乘以一個旋轉矩陣,則變換是共形的。
例:右圖1,直角格線(頂部)和它在共形映射 f下的像(底部)。可看出 f把以 90°相交的成對的線映射成仍以 90°相交的成對曲線。
定義
 共形映射
共形映射 共形映射
共形映射 共形映射
共形映射 共形映射
共形映射 共形映射
共形映射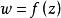 共形映射
共形映射 共形映射
共形映射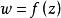 共形映射
共形映射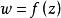 共形映射
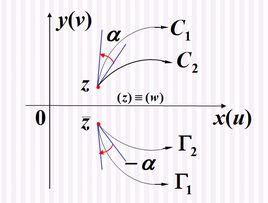
共形映射設函式 在 的鄰域內是一一映射的, 在 具有保角性和伸縮率不變性, 則稱映射 在 是保形的, 或稱 在 是保形映射. 如果映射 在D內的每一點都是保形的, 就稱 是區域D內的保形映射。
僅具有保角性和伸縮率不變性的映射稱為 第一類保角映射;而具有伸縮率不變性和保持角度絕對值不變而旋轉方向相反的映射稱為 第二類保角映射 。
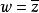 共形映射
共形映射例:是第二類保角映射。
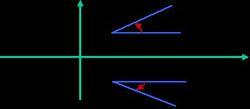 圖2.第二類保角映射圖例
圖2.第二類保角映射圖例定理
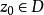 共形映射
共形映射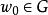 共形映射
共形映射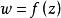 共形映射
共形映射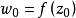 共形映射
共形映射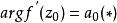 共形映射
共形映射定理一(黎曼定理)對邊界多於一點的任意兩個單連通域 D和 G,對任意給定的實數點 及 , 總唯一存在把D一一映射為G的 ,使得 , 。
定理二 (保域性)解析函式(不恆為常數)把區域映射為區域。
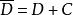 共形映射
共形映射定理三 (邊界對應原理)設區域 D的邊界為簡單閉曲線C,w=f(z)在 上解析,則將C一一映射為區域G的邊界 Γ,且保邊界方向。
製圖
在測繪學中,一個 共形變換投影是一個保持除有限點外所有點的角度不變的地圖投影。尺寸依賴於地點,但不依賴於方向。
其例子有麥卡托投影和極射投影。
複分析
共形映射很重要的一組例子來自複分析。若 U是一個複平面 C的開集,則一個函式
f : U → C是共形的,若且唯若它在U上是一個全純函式,而且它的導數處處非零。若 f是一個反全純函式(也就是全純函式的復共軛),它也保持角度,但是它會將定向反轉。
黎曼映射定理是複分析最深刻的定理之一,它表明任何 C的單連通非空開子集上有一個到 C中的開單位圓盤的雙射 。
套用
共形映射是複變函數論的一個分支,它從幾何的觀點來研究複變函數,其通過一個解析函式把一個區域映射到另一個區域進行研究。這個性質可以將一些不規則或者不好用數學公式表達的區域邊界映射成規則的或已成熟的區域邊界。共形映射的方法,解決了動力學,彈性理論,靜電場與磁場等方面許多實際問題,套用很廣 。
共形映射在數據擬合效果評價中的套用
共形映射可以將數據間很小的差異放大,使得圖件直觀性更好。映射後,擬合曲線將變成一個圓周,數據點也以一定的幅角分布在複數坐標上,能夠快速地判斷數據點位於哪兩個圓周形成的圓環範圍內; 經逆映射後,可以快速地找到實測數據點的上下限曲線方程 。
此外,共形映射最大的不足,就是需要事先基於擬合方程構造映射解析函式,這也是通過共形映射來評價數據擬合效果的前提條件之一 。
相關知識
•共形反常
•共形場論
•K-共形映射
•擬共形映射