簡介
考慮線性微分方程組
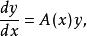 正則奇點
正則奇點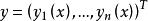 正則奇點
正則奇點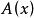 正則奇點
正則奇點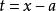 正則奇點
正則奇點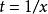 正則奇點
正則奇點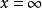 正則奇點
正則奇點 正則奇點
正則奇點自變數 x 取自複數域 D, 是 n 維復的列向量, 是以 x 的復解析函式為元素的 n 階方陣。由於通過平移 和自變數變化 可以分別將 x=a和 變到零點,所以不妨僅考慮點的奇異性。
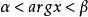 正則奇點
正則奇點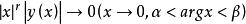 正則奇點
正則奇點對於上面方程的解 y(x) ,對於給定的任意角範圍,如果存在一個正數 r 使得,那么就稱 x=0 為方程的正則奇點,如果 x=0為方程的某個解的非正則奇點,那么就稱 x=0 為方程的非正則奇點(irregrlar singular point)。
對於二階齊線性微分方程
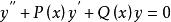 正則奇點
正則奇點 正則奇點
正則奇點 正則奇點
正則奇點 正則奇點
正則奇點 正則奇點
正則奇點 正則奇點
正則奇點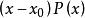 正則奇點
正則奇點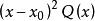 正則奇點
正則奇點 正則奇點
正則奇點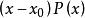 正則奇點
正則奇點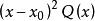 正則奇點
正則奇點 正則奇點
正則奇點而言,如果函式 P(x) 和 Q(x) 在 點附近是解析點,則稱這樣的點為該微分方程的常點。如果P(x) 或Q(x) 至少之一在點點解析性遭到破壞,則稱為該微分方程的奇點。如果是上述二階微分方程的奇點,但和 均為解析函式,則稱為該微分方程的正則奇點。反之,如果和至少之一為非解析,則稱為該微分方程的非正則奇點。
性質
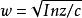 正則奇點
正則奇點一個與初值問題的初值有關的奇點稱為流動奇點(movable singular point) ,也就是說,隨著初值的改變,奇點可能消失,也可能奇性變強,奇點的位置依賴與特解的選擇。反之,如果奇點與初值無關,則稱為固定奇點(fixed singular point)。比如說,如果某方程的通解為 則 z=0 和 z=c 都是解的奇點,但 z=0是固定奇點,而 z=c 是流動奇點,有關奇點的幾個重要性質:
(1)(龐加萊定理)任何線性方程只有固定奇點沒有流動奇點;
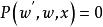 正則奇點
正則奇點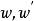 正則奇點
正則奇點(2)(潘勒韋定理)方程 的解沒有流動的本性奇點,其中 P 是 的多項式,且是 z 的解析函式;
(3)(富克斯定理)如果方程 dw/dz=R(w,z)沒有流動的本性奇點,其中 R(w,z)是 w 和 z 的有理函式,則該方程必為里卡蒂微分方程。
 正則奇點
正則奇點 正則奇點
正則奇點 正則奇點
正則奇點 正則奇點
正則奇點線上性二階常微分方程y''+p(x)y'+q(x)y=0的奇點的鄰域上,方程的兩個線性獨立解一般來說也是以為奇點的,對這兩個解在鄰域上展開(注意不是泰勒展開),全都具有有限個負冪項,則該奇點稱為方程的正則奇點。
奇點
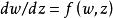 正則奇點
正則奇點一般來說,複平面上使方程 的右端函式或使此方程解的解析性遭到破壞的點就稱為奇點。也就是說,對於微分方程而言,奇點即可按方程右端函式的奇性分類,也可按方程解的奇性來分類。通常這兩種分類是相互獨立的,除非一些特殊系統,否則兩者之間沒有內蘊關係。
有關奇點點幾種常見分類有:正則奇點、非正則奇點、流動奇點、固定奇點等。