超幾何級數
當 c不是0,-1,-2...時,對於| z|<1,超幾何函式可用如下冪級數定義
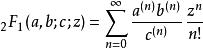 超幾何函式
超幾何函式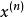 超幾何函式
超幾何函式其中 是Pochhammer符號,定義為:
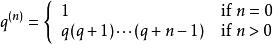 超幾何函式
超幾何函式當 a或 b是 0或負整數時級數只有有限項。
對於滿足| z|≥1 的複數 z,超幾何函式可以通過將上述在單位圓內定義的函式沿著避開支點 0和 1的任意路徑做解析延拓來得到。
特殊情形
很多普通的數學函式可以用超幾何函式或它的極限表示出來,一些典型的例子如下:
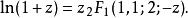 超幾何函式
超幾何函式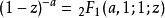 超幾何函式
超幾何函式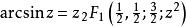 超幾何函式
超幾何函式合流超幾何函式(Kummer函式)可以用超幾何函式的極限表示如下
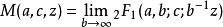 超幾何函式
超幾何函式因此,所有合流超幾何函式的特例,例如貝塞爾函式都可以表示成超幾何函式的極限。
勒讓德函式是有3個正則奇點的二階線性常微分方程的解,可以用以不同的形式用超幾何函式表示,例如
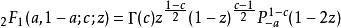 超幾何函式
超幾何函式很多多項式,例如賈可比多項式P(α,β)
n及其特殊情形勒讓德多項式,車比雪夫多項式,Gegenbauer多項式都能用超幾何函式表示
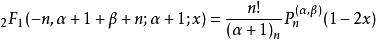 超幾何函式
超幾何函式其它特殊情形還包括Krawtchouk多項式,Meixner多項式,Meixner–Pollaczek多項式。
橢圓模函式有時能表示成參數 a, b, c是1, 1/2, 1/3, ... 或 0 的超幾何函式之比的反函式。例如,若
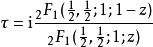 超幾何函式
超幾何函式則
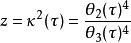 超幾何函式
超幾何函式是 τ的橢圓模函式.
不完整的beta函式 B( p, q) 表示成
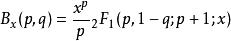 超幾何函式
超幾何函式完整的橢圓積分 K和 E如下給出
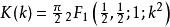 超幾何函式
超幾何函式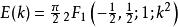 超幾何函式
超幾何函式超幾何方程
超幾何函式滿足的微分方程稱為 超幾何方程,其形式為(參見廣義超幾何函式)
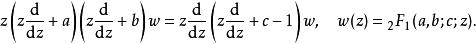 超幾何函式
超幾何函式展開後,得
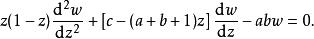 超幾何函式
超幾何函式它有三個正則奇點:0, 1, ∞.
變換公式
分式線性變換
Pfaff 變換
Pfaff 變換將正則奇點 1 和 ∞ 交換(也就是將李代數參數中的β與μ對換):
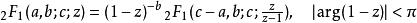 超幾何函式
超幾何函式由a,b的對稱性自然有:
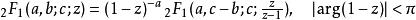 超幾何函式
超幾何函式Euler 變換
Pfaff 變換可以導出 Euler 變換,它將李代數參數β變成 -β:
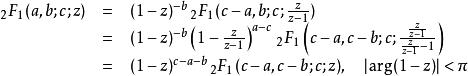 超幾何函式
超幾何函式Pfaff 變換和 Euler 變換都是分式線性變換的例子,這得名於等式兩邊的超幾何函式的宗量的聯繫,參見莫比烏斯變換。
將上面提到的四個連線關係與 Pfaff 變換及 Euler 變換組合起來,就得到完整的 Kummer 表。
給定一組李代數參數(α,β,μ),(±α,±β,±μ) 及其輪換對應著 24 個不同但彼此關聯的超幾何函式(F恆等於F),利用前面提到的四個連線關係和 Pfaff 變換,它們中的任意一個可以通過任意另外兩個表出。
例如 Euler 變換可以表示為:
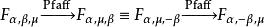 超幾何函式
超幾何函式二次變換
下面是一個二次變換的例子:
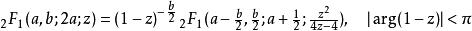 超幾何函式
超幾何函式二次變換得名於等號兩邊超幾何函式宗量的聯繫(一個二次函式和一個莫比烏斯變換的組合)。
三次高次變換
若一組李代數參數滿足下列條件:有兩個是 ±1/3,或者三個參數的絕對值相等,則有一個三次變換的公式將它與另一個超幾何函式聯繫起來。
另外有一些 4 次和 6 次變換的公式。其它次數的變換公式只有當參數取特定有理數值時存在。

