定寬曲線

定寬曲線的概念指具有（類似圓的）定寬性的曲線。 定寬曲線的舉例:圓形、勒洛三角形、月亮、圓球（太陽） 作一個等邊三角形ABC，然後以頂點A為圓心，三角形邊長為半徑，做弧連線BC點，再以頂點B為圓心，三角形邊長為半徑，做弧連線AC點，再以頂點C為圓心，三角形邊長為半徑，做弧連線AB點，則曲線ABC就是勒洛三角形。勒洛三角形不是圓，可它在每個方向上的寬度都等於正三角形的邊長。用它的形狀做成滾輪，和圓形滾輪的效果是一樣。

基本信息

• 中文名：定寬曲線

• 釋義：具有（類似圓的）定寬性的曲線
• 代表：勒洛三角形、月亮 、圓球
• 學科：數學

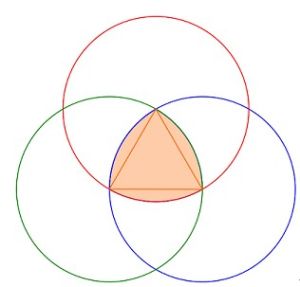
實例

用圓作車輪是人類文明發展過程中選擇的結果，不僅由於圓的定寬性，還由於圓是最常見的圖形之一，比如太陽，月亮等，也是所有定寬曲線中最簡單的。圓形較為容易加工。而且定寬的穩定性較好，即使圓形不算正規，還會保持較好的定寬性。

人們將車輪做成圓形，是利用了圓的一個重要性質：將一個圓放在兩條平行線中間，使之與這兩平行線相切。則可以做到：無論這個圓如何運動，它還是在這兩條平行線內，並且始終與這兩條平行線相切。此即圓的定寬性質，具有類似圓的定寬性質的曲線稱為定寬曲線。

另外，圓形還具有一條重要的性質，幾何中心的穩定性，圓的中軸（過圓心的軸）在圓轉動的時候是保持高度不變的，始終是地面往上半徑的高度。

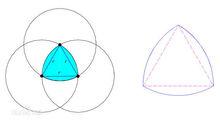萊洛三角形

弧三角形,又叫勒洛三角形, 是機械學家勒洛首先進行研究的。弧三角形是這樣畫的;先畫正三角，然後分別以三個頂點為圓心,邊長長為半徑畫弧得到的三角形。

性質

幾何上的理解是：將一個圓放在兩條平行線中間，使之與這兩平行線相切。則可以做到：無論這個圓如何運動，它還是在這兩條平行線內，並且始終與這兩條平行線相切。
定寬性與穩定性類似。