漸開線

漸伸線（involute）(或稱漸開線(evolent))和漸屈線（evolute）是曲線的微分幾何上互為表里的概念。若曲線A是曲線B的漸伸線，曲線B是曲線A的漸屈線。在曲線上選一定點S。有一動點P由S出發沿曲線移動，選在P的切線上的Q，使得曲線長SP和直線段長PQ相同。漸伸線就是Q的軌跡。若曲線B有參數方程，其中，曲線A的方程為。曲線的漸屈線是該曲線每點的曲率中心的集。若該曲線有參數方程（），則其漸屈線為每條曲線可有無窮多條漸伸線，但只有一條漸屈線。

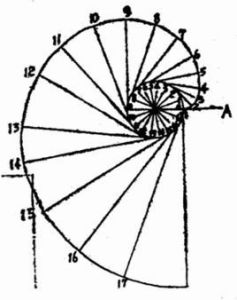
解釋

將一個圓軸固定在一個平面上，軸上纏線，拉緊一個線頭，讓該線繞圓軸運動且始終與圓軸相切，那么線上一個定點在該平面上的軌跡就是漸開線。

直線在圓上純滾動時，直線上一點K的軌跡稱為該圓的漸開線，該圓稱為漸開線的基圓，直線稱為漸開線的發生線。 漸開線的形狀僅取決於基圓的大小，基圓越小，漸開線越彎曲；基圓越大，漸開線越平直；基圓為無窮大時，漸開線為斜直線。漸開線方程為：

x=r×cos(θ+α)+(θ+α)×r×sin(θ+α)

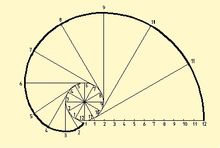漸開線畫法

y=r×sin(θ+α)-(θ+α)×r×cos(θ+α)

z=0

式中，r為基圓半徑；θ為展角，其單位為弧度

展角θ和壓力角α之間的關係稱為漸開線函式

θ=inv(α)=tan(α)-α

式中，inv為漸開線involute的縮寫

畫法

已知圓的直徑D，畫漸開線的方法如圖

(1）將圓周分成若干等分（圖中為12等分），將周長πD作相同等分；

(2）過周長上各等分點作圓的切線；

(3）在第一條切線上，自切點起量取周長的一個等分（πD/12）得點1；在第二條切線上，自切點起量取周長的兩個等分（2xπD/12）得點2；依此類推得點3、4、……、12；

(4）用曲線板光滑連線點1、2、3、……、12；即得圓的漸開線。

直線在圓上純滾動時，直線上一點K的軌跡稱為該圓的漸開線，該圓稱為漸開線的基圓，直線稱為漸開線的發生線。