定義
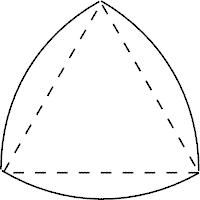
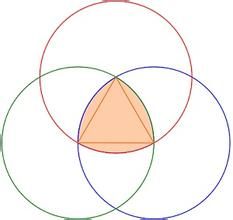
勒洛三角形是由德國機械工程專家,機構運動學家勒洛(出生於1829,死於1905)首先發現,所以以他的名字命名。作法:以等邊三角形每個頂點為圓心,以邊長為半徑,在另兩個頂點間作一段弧,三段弧圍成的曲邊三角形就是勒洛三角形。性質
 勒洛三角形
勒洛三角形定寬性,幾何上的理解是:將一個圓放在兩條平行線中間,使之與這兩平行線相切。則可以做到:無論這個圓如何運動,它還是在這兩條平行線內,並且始終與這兩條平行線相切。
勒洛三角形就是典型的定寬曲線。
勒洛三角形的等寬性質很容易證明,其寬度等於構造等邊三角形的邊長。當勒洛三角形在邊長為其寬度的正方形內鏇轉時,每一個角走過的軌跡基本上就是一個正方形。
面積關係
通過勒貝格積分可以算出,勒洛三角是定寬曲線所能構成的面積
最小的圖形,其面積為1/2[π-(3^1/2)]s^2,s為定寬寬度。
勒洛三角形的套用
在美國舊金山,有一些市政檢修井井蓋的形狀就是勒洛三角形,其最大優點是這種形狀的井蓋絕不會掉到井裡去。
此外,一種基於勒洛三角形的變體的設備,它能鑽出方孔來,其“方度”非常之好。
勒洛不能用作輪子,因為其中心並不穩定,每鏇轉一圈會有三次跳動。而作為滾軸使用則是相當平穩。馬自達的轉子發動機也是這個原理,因為勒洛三角形是定寬曲線中面積最小的。