定理內容
多項式餘數定理即餘數定理，內容是一個多項式f(x)除以(x-a)的餘數等於f(a)。
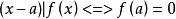多項式餘數定理推論：
推廣形式
設a,a,…,a是 n 個不同的數，而 F(x)=(x-a)(x-a)…(x-a)，對任意多項式 f(x)用F(x)除所得 的餘式為
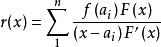多項式餘數定理證明
根據除法的定義及性質可知，被除數=除數×商+餘數。
設多項式P(x) 除以一次式(x-a) 所得的商為Q(x) ，餘數為R ，根據上面的性質可以列出下列恆等式令P(x) =(x-a)*Q(x) +R，令x=a代入上式即得P(a)=P(a-a)*Q(a)+R ，因此得到結論：P(x)除以(x-a) 後的餘數R=P(a) 。
注意：若除式不為(x-a) 的類型，依然可以利用上面的方法來求餘數（式），即先求出使除式為0的x的值，再代入恆等號兩邊。
例題
例4、確定m的值使多項式f(x)=x -3x +8x +11x+m能夠被x-1整除。
解：依題意f(x)含有因式x-1，故f(1)=0。
∴1-3+8+11+m=0。可得m=－17。
求一個關於x的二次多項式，它的二次項係數為1，它被x-3除餘1，且它被x-1除和被x-2除所得的餘數相同。
解：設f(x)=x +ax+b
∵f(x)被x-3除餘1，
∴f(3)=9+3a+b=1①
∵f(X)被(X-1)除和(x-2)除所得的餘數相同，
∴ f(1)=f(2)即1+a+b=4+2a+b②
由②得a=-3，代入①得b=1
∴f(x)=x -3x+1。
註：本例也可用待定係數法來解。同學們不妨試一試。
