陳述
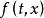瑪爾格朗日預備定理
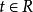瑪爾格朗日預備定理
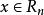瑪爾格朗日預備定理假設是原點附近的和的平滑複函數，並且令k為最小整數，使得
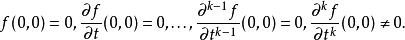瑪爾格朗日預備定理然後，準備定理的一種形式表明，原點f附近可以寫為在原點處非零的平滑函式c和作為t的函式的平滑函式的乘積是k的多項式。 換一種說法，
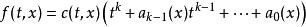瑪爾格朗日預備定理函式c和a是平滑的，c在原點是非零的。
定理的第二種形式，偶爾稱為馬瑟分裂定理，是一種“餘數除法”定理：它說如果f和k滿足上述條件而g是原點附近的平滑函式，那么我們就可以寫
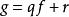瑪爾格朗日預備定理其中q和r是平滑的，並且作為t的函式，r是小於k的多項式。這意味著
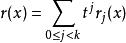瑪爾格朗日預備定理
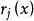瑪爾格朗日預備定理對於一些平滑函式。
定理的兩種形式容易相互暗示：第一種形式是“餘數除法”形式的特殊情況，其中g是tk，而餘數形式的除法遵循定理的第一種形式，因為我們可以假設作為t的函式的f是k次多項式。
如果函式f和g是實數，那么函式c，a，q和r也可以被認為是真實的。在Weierstrass準備定理的情況下，這些函式由f和g唯一確定，但對於瑪爾格朗日預備定理，唯一性不再適用 。
定理的證明
瑪爾格朗日預備定理可以從Weierstrass預備定理推導出來。這樣做的明顯方法不起作用：雖然平滑函式在原點具有正式的冪級數展開，而Weierstrass預備定理適用於形式冪級數，但形式冪級數通常不會收斂到原點附近的平滑函式。相反，人們可以通過將單位分區套用於其傅立葉變換來使用將平滑函式分解為解析函式之和的思想。有關這些方面的證據，請參閱(Mather 1968)或 (Hörmander 1983a, 第7.5節）
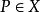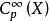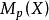代數版的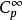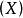瑪爾格朗日預備定理
瑪爾格朗日預備定理
瑪爾格朗日預備定理
瑪爾格朗日預備定理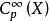 瑪爾格朗日預備定理
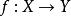瑪爾格朗日預備定理
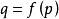瑪爾格朗日預備定理
瑪爾格朗日預備定理
瑪爾格朗日預備定理 瑪爾格朗日預備定理
瑪爾格朗日預備定理 瑪爾格朗日預備定理
瑪爾格朗日預備定理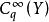
瑪爾格朗日預備定理
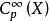瑪爾格朗日預備定理 瑪爾格朗日預備定理 瑪爾格朗日預備定理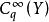
瑪爾格朗日預備定理 瑪爾格朗日預備定理 瑪爾格朗日預備定理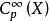 瑪爾格朗日預備定理 瑪爾格朗日預備定理 瑪爾格朗日預備定理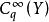 瑪爾格朗日預備定理 瑪爾格朗日預備定理 瑪爾格朗日預備定理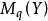
瑪爾格朗日預備定理瑪爾格朗日預備定理可以作為關於平滑，實值細菌環的模組的定理來重述。如果是具有的流形，則讓表示在上的處的平滑函式的實值細菌的環。設表示的唯一最大理想，由在消失的細菌組成。設是 - 模，讓是流形之間的平滑函式。設。通過右側的組合誘導環同態 *：→。因此，我們可以將視為模組。然後瑪爾格朗日預備定理說如果是有限生成的模組，則是有限生成的模組，若且唯若 /是有限維實數向量空間。
