目錄
1.數學專著介紹
2.研究論文介紹
(1)論文摘要
(2)論文引言
(3)論文正文
(4)參考文獻
3.研究論文說明
1.數學專著介紹
數學專著書名,胡振武著,2007年9月自費印刷,全書手寫,16開126頁。內容為作者自1970年代末開始對費馬大定理的研究,及1984年撰寫的研究論文,稱作“世界的費馬大定理,中國人的簡要證明”。書中比較詳細地介紹了前人的研究成果,包括我國數學家蔣春暄及英國數學家懷爾斯的證明。作者出版的目的是“向世人留下我的證明,留下我向諸位專家方家大家請教的真誠”,“自費出版,不為名,不為利,是請別人挑個刺,給自己留個記”。該書在國家圖書館上海圖書館浙江圖書館及各著名大學圖書館有收藏,在國外各著名國家圖書館各著名大學圖書館有收藏。
2.研究論文介紹
(1)論文摘要p次費馬方程證明
胡振武
摘要本文將帶餘數除法定理、多項式恆等定理、費馬小定理相結合,使p次費馬方程由難以計算的不確定狀態變成可以計算的確定狀態,從而證明費馬大定理成立,經過歷史資料檢索,前人沒有先例。
關鍵字費馬大定理(FLT)證明
中圖分類O156
1引言
1637年,費馬提出:“將一個立方數分為兩個立方數,一個四次冪分為兩個四次冪,或者一般地將一個高於二次的冪分為兩個同次的冪,這是不可能的。”即方程

1992年,蔣春暄用p階和4n階復雙曲函式證明FLT。
1994年,懷爾斯用模形式、谷山—志村猜想、伽羅瓦群等現代數學方法間接證明FLT,但是他的證明明顯與費馬構想的證明不同。
據前人研究,任何一個大於2的正整數n,或是4的倍數,或是一個奇素數的倍數,因此證明FLT,只需證明兩個指數n=4及n=p時方程沒有正整數解即可。方程
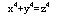
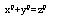
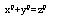
又據前人研究,為了證明的方便,經常把FLT分為兩種情形。第一種情形,對於素指數p,不存在x、y、z,使p⊥xyz且
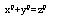
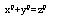
本文將帶餘數除法定理、多項式恆等定理、費馬小定理相結合,使p次費馬方程由難以計算的不確定狀態變成可以計算的確定狀態,從而證明FLT成立。經過歷史資料檢索,如此新穎證法,前人沒有先例。(3)論文正文
2證明
(4)參考文獻3.研究論文說明
論文p次費馬方程證明的說明
胡振武
費馬提出:方程X+Y=Z,當正整數指數n﹥2時,沒有正整數解。當然xyz=0除外。這就是費馬大定理(FLT)。FLT方程是不定方程,數列無窮大,難以計算。為避免無窮大和便於計算,前人把FLT方程變形為X+Y= 1,有人稱之為費馬方程,此時方程解的集合的圖象稱為費馬曲線,這已有違費馬的原意。弗賴將三維高次的FLT方程變形為二維三次的橢圓方程更有違費馬的原意。而懷爾斯是藉助弗賴橢圓方程的推斷,間接證明FLT,顯然與費馬原來的構想是不相同的。如果FLT是世界高峰,那么通往這個高峰的道路可能不止一條,但總有一條路較好。前人證明特定條件下的FLT方程沒有正整數解;我則給出一般性普遍性的證明,並且說明n=2時有正整數解是此一般性證明中的一個特例,故可以說給出的是數學追求的滿意解。包含有費馬小定理和無窮遞降法的那種證法可能復原重現費馬的思路。論文p次費馬方程證明是我的證明之一。我的證明詳見拙著《費馬大定理證明之研究》(中文稿,目錄及論文有英文),此書在各著名國家圖書館和各著名大學圖書館裡可以查閱。
