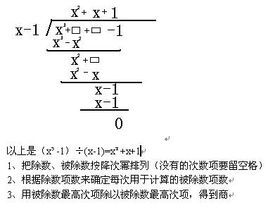
一般步驟
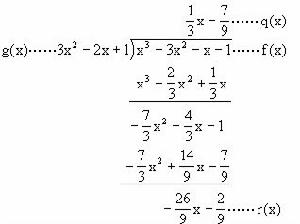多項式除法示例多項式除以多項式一般用豎式進行演算
（1）把被除式、除式按某個字母作降冪排列，並把所缺的項用零補齊．
（2）用被除式的第一項去除除式的第一項，得商式的第一項．
（3）用商式的第一項去乘除式，把積寫在被除式下面（同類項對齊），消去相等項，把不相等的項結合起來．
（4）把減得的差當作新的被除式，再按照上面的方法繼續演算，直到餘式為零或餘式的次數低於除式的次數時為止．被除式=除式×商式+餘式。
舉例
計算把被除式、除式按某個字母作降冪排列，並把所缺的項用零補齊，寫成以下這種形式：
然後商和餘數可以這樣計算：
將分子的第一項除以分母的最高次項（即次數最高的項，此處為x）。結果寫在橫線之上(x3÷x=x2).
將分母乘以剛得到結果（最終商的第一項），乘積寫在分子前兩項之下（同類項對齊）(x2·(x−3)=x3−3x2).
從分子的相應項中減去剛得到的乘積（消去相等項，把不相等的項結合起來），結果寫在下面。((x3−12x2)−(x3−3x2)=−12x2+3x2=−9x2)然後，將分子的下一項“拿下來”。
把減得的差當作新的被除式，重複前三步（直到餘式為零或餘式的次數低於除式的次數時為止．被除式=除式×商式+餘式）
重複第四步。這次沒什麼可以“拿下來”了。
橫線之上的多項式即為商，而剩下的(−123)就是餘數。
算數的長除法可以看做以上算法的一個特殊情形，即所有x被替換為10的情形。
整除
如果一個多項式除以另一個多項式，餘式為零，就說這個多項式能被另一個多項式整除。套用
多項式的因式分解
有時某個多項式的一或多個根已知，可能是使用有理根定理（Rationalroottheorem）得到的。如果一個次多項式的一個根已知，那么可以使用多項式長除法因式分解為的形式，其中是一個次的多項式。簡單來說，就是長除法的商，而又知是的一個根、餘式必定為零。相似地，如果不止一個根是已知的，比如已知和這兩個，那么可以先從中除掉線性因子得到，再從中除掉，以此類推。或者可以一次性地除掉二次因子。
使用這種方法，有時超過四次的多項式的所有根都可以求得，雖然這並不總是可能的。例如，如果有理根定理（Rationalroottheorem）可以用來求得一個五次方程的一個（比例）根，它就可以被除掉以得到一個四次商式；然後使用四次方程求根的顯式公式求得剩餘的根。
