定義
多項式函式與多項式
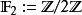 多項式環
多項式環在初等數學與微積分中, 多項式視同 多項式函式,兩者在一般的域或環上則有區別。舉例言之,考慮有限域 上的多項式
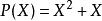 多項式環
多項式環此多項式代任何值皆零,故給出零函式,但其形式表法非零。
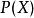 多項式環
多項式環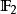 多項式環
多項式環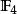 多項式環
多項式環我們寧願將多項式看作形式的符號組合,以得到較便利的代數理論。且考慮多項式在域擴張之下的性質:就函式觀點,多項式函式在域擴張下的行為頗複雜,上述 給出 上的零函式,但視為 上的多項式函式則非零;而就形式觀點,只須將係數嵌入擴張域即可。
形式定義
於是我們採取下述定義:令R 為環。一個單變元X 的多項式 P(X)定義為下述形式化的表法:
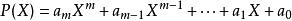 多項式環
多項式環 多項式環
多項式環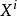 多項式環
多項式環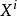 多項式環
多項式環其中 屬於R,稱作 的 係數,而X 視作一個形式符號。兩多項式相等若且唯若每個 的係數均相同。次數最大的非零係數稱為該多項式的 領導係數,或者 首項係數。
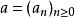 多項式環
多項式環更嚴謹的說法或許是將多項式定義為係數的序列 ,使得其中僅有有限項非零。但是我們在實踐上總是用變元 X及其冪次表達。
多項式的運算
以下固定環 R,我們將推廣初等數學中熟悉的多項式運算。
環結構
多項式的加法由係數逐項相加定義,而乘法則由下列法則唯一地確定:
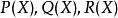 多項式環
多項式環分配律:對所有R上的多項式 ,恆有
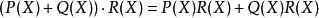 多項式環
多項式環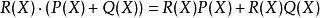 多項式環
多項式環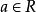 多項式環
多項式環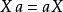 多項式環
多項式環對所有 ,有
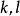 多項式環
多項式環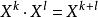 多項式環
多項式環對所有非負整數 ,有
運算的具體表法如下:
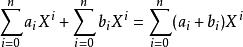 多項式環
多項式環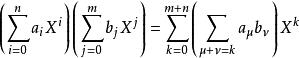 多項式環
多項式環當 R 是交換環時,R[X] 是個 R 上的代數。
多項式的合成
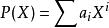 多項式環
多項式環設 而Q(X) 為另一多項式,則可定義兩者的 合成為
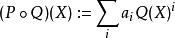 多項式環
多項式環求值
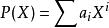 多項式環
多項式環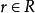 多項式環
多項式環對於任一多項式 及 ,我們可考慮 P(X) 對r的 求值:
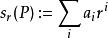 多項式環
多項式環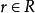 多項式環
多項式環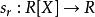 多項式環
多項式環固定 ,則得到一個環同態 ,稱作求值同態;此外它還滿足
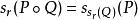 多項式環
多項式環導數
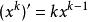 多項式環
多項式環在微積分中,多項式的微分由微分法則 確定。雖然一般的環上既無拓撲結構更無完備性,我們仍然可形式地定義多項式的導數為:
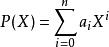 多項式環
多項式環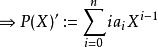 多項式環
多項式環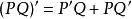 多項式環
多項式環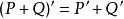 多項式環
多項式環這種導數依然滿足 與 等性質。對於係數在域上的多項式,導數也可以判定重根存在與否。
多變元的情形
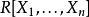 多項式環
多項式環上述定義可以推廣到任意個變元(包括無限個變元)的情形。對於有限變元的多項式環 ,也可以採下述構造:
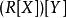 多項式環
多項式環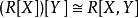 多項式環
多項式環先考慮兩個變元 X,Y 的例子,我們可以先構造多項式環R[X],其次構造 。可以證明有自然同構 ,例如多項式
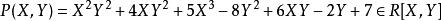 多項式環
多項式環也可以視作
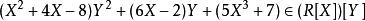 多項式環
多項式環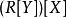 多項式環
多項式環對 亦同。超過兩個變元的情形可依此類推。
性質
若 R是域,則 R[X] 是主理想環(事實上還是個歐幾里得整環)。
若 R是唯一分解環,則 R[X] 亦然。
若 R是整環,則 R[X]亦然。
若 R是諾特環,則 R[X] 亦然;這是希爾伯特基底定理的內容。
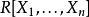 多項式環
多項式環任一個交換環R上的有限生成代數皆可表成某個 的商環。
數學中的角色
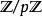 多項式環
多項式環多項式環對理想的商是構造環的重要技術。例子包括從同餘系 構造有限域,或從實數構造複數等等。
弗羅貝尼烏斯多項式是另一個跟多項式環相關的環,此環的乘法系採用多項式的合成而非乘法。

