定義
諾特模是一種重要的模。它是阿廷模的對偶概念。即滿足極大條件的模。若A模M的任一子模升鏈M1M2…都是有限終止的,即存在n,使得Mn=Mn+1=…,則稱模M滿足升鏈條件。模M是諾特模的充分必要條件是它滿足升鏈條件;也等價於,M的每個子模是有限生成的。若將環A看做左A模時它是諾特模,則稱A是左諾特環(關於右的情形完全類似)。諾特環是一類概括廣的重要環,它在代數幾何等學科中有很大的套用價值。域上的多元多項式及其商環(因而代數曲線、代數曲面的坐標環)都是諾特環。
阿廷模
與諾特模對偶的概念,即滿足極小條件的模。若A模M的任一子模降鏈MM…都是有限終止的,即存在n,使得M=M=…,則稱模M滿足降鏈條件。模M是阿廷模的充分必要條件是它滿足降鏈條件。若將環A看做左A模時它是阿廷模,則稱環A是左阿廷環(關於右的情形完全類似)。有單位元的阿廷環一定是諾特環。
諾特環
設R是一個有單位元的交換環,如果R的每個理想鏈I⫅I⫅I⫅…都存在整數n,使得對任何i≥n,I=I,則稱R是一個諾特環。設R是一個交換環,R的理想Q稱為準素理想,如果Q≠R,對任意的a,b∈R,若ab∈Q,a∉Q,則必存在正整數n,使得b∈Q。設I是交換環R的理想,I的根(或稱冪零根)是包含I的所有素理想之交,記作或radI。準素理想的根是一個素理想,這個素理想稱為與Q結合的素理想,或Q是屬於這個素理想的準素理想。交換環R中的理想I稱為有準素分解,如果I=Q∩…∩Q,其中Q,i=1,…,n都是準素理想。如果每個Q都不包含 Q∩…∩Q∩Q∩…∩Q,而且Q的根互不相同,則稱這樣的準素分解是既約的。一個有單位元的交換環R是諾特環若且唯若R的每個理想是有限生成的,若且唯若R滿足理想的極大條件:對R的任一個理想的非空族{I},其中必存在極大元I,即若J∈ {I},I⫅J,則I=J。含麼交換環是諾特環若且唯若每個素理想是有限生成的。諾特環R的每個理想I,I≠R,有準素分解,而且若I=A∩…∩A,I=B∩…∩B是兩個既約準素分解,其中A是屬於P的準素理想,B是屬於Q的準素理想,則n=m,而且適當重排順序後,P=Q。環R的非空子集S稱為R的一個乘閉子集,如果對任何a,b∈S,ab∈S。設S是交換環R的一個乘閉子集,在集合R×S上定義一個關係~: (r,s) ~ (r′,s′),如果存在S∈S使得s(rs′-r′s) =0,這個關係是一個等價關係,(r,s)所在等價類記作r/s,R×S的全體等價類做成的集合記作SR,在SR中定義則SR做成一個有單位元的交換環。SR稱為R對於S的分式環。一個有單位元的交換環稱為局部環,如果它只有一個極大理想。設R是有單位元的交換環,P是R的素理想,令S=R\P,則S是R的乘閉子集,分式環SR是一個局部環,稱為R在P處的局部化,記作R。設S是諾特環R的乘閉子集,則SR也是諾特環。設R是—個諾特環,R[x,…,x]是R上文字x,…,x的多項式全體做成的環,則R[x,…,x]也是諾特環,這個結論稱為希爾伯特基定理。設R是一個諾特環,R[[x]]是R上文字x的形式冪級數全體做成的環,則R[[x]]也是諾特環。
性質
模M是諾特的,若且唯若M的任意子模是有限生成的A模。
1.模M是諾特的,若且唯若M的任意子模是有限生成的A模。
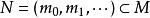 諾特模
諾特模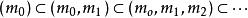 諾特模
諾特模證明:=>否則不妨設,那么為無窮升鏈,與M是諾特的相矛盾。
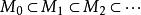 諾特模
諾特模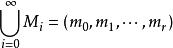 諾特模
諾特模<=如果存在無窮升鏈,考慮即可導致矛盾。
2. 模M是諾特的,若且唯若對於M的任意自模N,N和M/N均為諾特模。
證明:=>若M是諾特的,顯然N也是諾特的。對於M/N的任意自模,唯一對應了一個包含N的M自模,因此易知其也為諾特的。
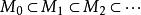 諾特模
諾特模<=對於M的任意上升鏈,我們考察如下兩個升鏈
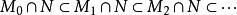 諾特模
諾特模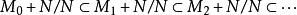 諾特模
諾特模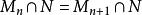 諾特模
諾特模 諾特模
諾特模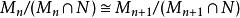 諾特模
諾特模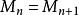 諾特模
諾特模顯然存在r使得當n>r時有且,對於第二項我們用群同構定理可知,又由第一項我們有。
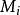 諾特模
諾特模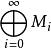 諾特模
諾特模推論1:如果是諾特的,那么也是諾特的。
推論2:如果R是諾特環,那么其上的有限生成模是諾特的。
